题目内容
 附加题:对于本试卷第19题:“图中△ABC外接圆的圆心坐标是”.请再求:
附加题:对于本试卷第19题:“图中△ABC外接圆的圆心坐标是”.请再求:(1)该圆圆心到弦AC的距离;
(2)以BC为旋转轴,将△ABC旋转一周所得几何体的全面积.(所有表面面积之和)
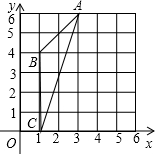
分析:(1)如图,圆心为P(5,2),作PD⊥AC于D,根据垂径定理知道AD=CD,然后利用图中小正方形可以求出AC,再求出PD,也可直接求出PD;
(2)根据旋转过程可以知道旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥,再挖掉一个以2为底面圆半径、2为高的小圆锥,它们的母线分别是AB,AC,可以利用小正方形求出,圆锥的侧面展开图是扇形,利用扇形的面积公式就可以求出全面积了.
(2)根据旋转过程可以知道旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥,再挖掉一个以2为底面圆半径、2为高的小圆锥,它们的母线分别是AB,AC,可以利用小正方形求出,圆锥的侧面展开图是扇形,利用扇形的面积公式就可以求出全面积了.
解答: 解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
连接CP,∵AC为是为6、宽为2的矩形的对角线,
∴AC=
=2
,(2分)
同理CP=
=2
,(3分)
∴PD=
=
,(4分)
方法2:
∵圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
由直观,发现点D的坐标为(2,3)(2分)
又∵PD是长为3、宽为1的矩形的对角线,
∴PD=
=
.(4分)
(2)∵旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥,再挖掉一个以2为底面圆半径、2为高的小圆锥,
又它们的母线之长分别为ι小=
=2
,ι大=
=2
,(7分)
∴所求的全面积为:πrι大+πrι小(8分)
=πr(ι大+ι小)
=4(
+
)π. (9分)
 解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
解:方法1:如图,圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)连接CP,∵AC为是为6、宽为2的矩形的对角线,
∴AC=
| 62+22 |
| 10 |
同理CP=
| 42+22 |
| 5 |
∴PD=
| CP2-CD2 |
| 10 |
方法2:
∵圆心为P(5,2),作PD⊥AC于D,则AD=CD,(1分)
由直观,发现点D的坐标为(2,3)(2分)
又∵PD是长为3、宽为1的矩形的对角线,
∴PD=
| 32+12 |
| 10 |
(2)∵旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥,再挖掉一个以2为底面圆半径、2为高的小圆锥,
又它们的母线之长分别为ι小=
| 22+22 |
| 2 |
| 22+62 |
| 10 |
∴所求的全面积为:πrι大+πrι小(8分)
=πr(ι大+ι小)
=4(
| 10 |
| 2 |
点评:此题要充分发挥小正方形的作用--利用它求图中的线段长,然后就可以求出题目的结论;也要求掌握旋转的图形变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



