题目内容
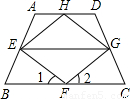
(2004•茂名)已知:如图,点E、F、G、H分别是梯形ABCD四条边上的中点,AD∥BC,AB=CD=EG=4.(1)求梯形ABCD的周长;
(2)∠1与∠2是否相等?为什么?
(3)求证:四边形EFGH是菱形.
【答案】分析:(1)根据梯形的中位线定理得到梯形的上下底的和,进一步求得梯形的周长;
(2)根据等腰梯形的性质和全等三角形的判定进行证明,从而得到两个角相等;
(3)连接对角线.根据梯形的中位线定理,可以得到该四边形的每一条边都是对角线的一半,结合对角线相等,即可证明该四边形的四条边都相等,从而证明是菱形.
解答: 解:(1)由已知,得:EG是梯形的中位线,
解:(1)由已知,得:EG是梯形的中位线,
∴AD+BC=2×4=8,
∴梯形ABCD的周长=AD+BC+CD+AD,
=4+4+8=16;
(2)∠1=∠2
由已知得:EB=GC= AB,BF=CF=
AB,BF=CF= BC,
BC,
而AB=CD,∴∠B=∠C,
∴△EBF≌△GCF
∴∠1=∠2;
(3)证法一:连接AC、BD,
在梯形ABCD中,AB=CD,∴AC=BD
在△ABD中,∵点E、H分别为AB、AD的中点,
∴EH= BD,
BD,
同理:FG= BD,EF=
BD,EF= AC,GH=
AC,GH= AC,
AC,
∴EF=FG=GH=HE= BD,
BD,
∴四边形EFGH是菱形.
点评:熟练运用梯形的中位线定理.注意:顺次连接对角线相等的四边形各边中点所得的四边形是菱形.
(2)根据等腰梯形的性质和全等三角形的判定进行证明,从而得到两个角相等;
(3)连接对角线.根据梯形的中位线定理,可以得到该四边形的每一条边都是对角线的一半,结合对角线相等,即可证明该四边形的四条边都相等,从而证明是菱形.
解答:
 解:(1)由已知,得:EG是梯形的中位线,
解:(1)由已知,得:EG是梯形的中位线,∴AD+BC=2×4=8,
∴梯形ABCD的周长=AD+BC+CD+AD,
=4+4+8=16;
(2)∠1=∠2
由已知得:EB=GC=
 AB,BF=CF=
AB,BF=CF= BC,
BC,而AB=CD,∴∠B=∠C,
∴△EBF≌△GCF
∴∠1=∠2;
(3)证法一:连接AC、BD,
在梯形ABCD中,AB=CD,∴AC=BD
在△ABD中,∵点E、H分别为AB、AD的中点,
∴EH=
 BD,
BD,同理:FG=
 BD,EF=
BD,EF= AC,GH=
AC,GH= AC,
AC,∴EF=FG=GH=HE=
 BD,
BD,∴四边形EFGH是菱形.
点评:熟练运用梯形的中位线定理.注意:顺次连接对角线相等的四边形各边中点所得的四边形是菱形.

练习册系列答案
相关题目
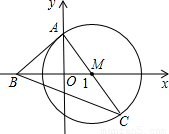
 的圆与y轴交于A、D两点.
的圆与y轴交于A、D两点. ,抛物线y=ax2+bx+c经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.
,抛物线y=ax2+bx+c经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.
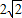 的圆与y轴交于A、D两点.
的圆与y轴交于A、D两点.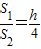 ,抛物线y=ax2+bx+c经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.
,抛物线y=ax2+bx+c经过B、M两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式.