题目内容
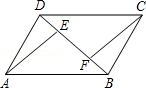
如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=12，BD=5，则这个梯形中位线的长等于 ．
。【考点】三角形和梯形中位线定理，平行四边形的判定和性质，勾股定理。
如图，作DE∥AC，交BC的延长线于E，则四边形ACED为平行四边形，
∴AD=CE。
∵AC⊥BD∴∠BDE=90°。
∴梯形的中位线长=
（AD+BC）=（CE+BC）=BE。
∵AC=12，BD=5，∴
。
∴梯形的中位线长=×13=。
∴AD=CE。
∵AC⊥BD∴∠BDE=90°。
∴梯形的中位线长=
（AD+BC）=（CE+BC）=BE。∵AC=12，BD=5，∴
。∴梯形的中位线长=
×13=。
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
为平行四边形ABCD的对角线，
为
于点
，
分别交于点
．求证：⑴
．⑵
，BC=4，连结BD，∠BAD的平分线交BD于点E，且AE∥CD，则AD的长为【 】
，求AB的长。