��Ŀ����
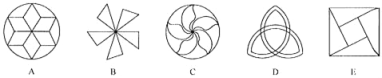
����Ŀ����1��ָ��������ת�Գ�ͼ�ε���С��ת�ǣ�����ͼ�б���������ת����O��
��2������������ͼ������û�����ĶԳ�ͼ�Σ�����ָ�����ļ�����
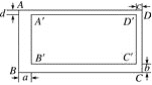
�⣺ͼ��A����С��ת������ ���ȣ����� �����ĶԳ�ͼ�Σ�
ͼ��B����С��ת������ ���ȣ����� �����ĶԳ�ͼ�Σ�
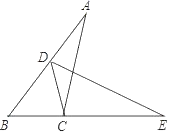
ͼ��C����С��ת������ ���ȣ����� �����ĶԳ�ͼ�Σ�
ͼ��D����С��ת������ ���ȣ����� �����ĶԳ�ͼ�Σ�
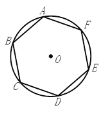
ͼ��E����С��ת������ ���ȣ����� �����ĶԳ�ͼ�Σ�
���𰸡���1�������������2��60���ǣ�72�����ǣ�72�����ǣ�120�����ǣ�90���ǣ�
��������
��1��һ��ͼ��Χ��ijһ����תһ���ĽǶȣ�С��360����������ԭͼ���غϣ���ô���ͼ�ξͽ�����ת�Գ�ͼ�Σ�
��2��һ��ͼ����ijһ����ת180���������ת���ͼ���ܹ���ԭ����ͼ���غϣ���ô���ͼ�ξͽ������ĶԳ�ͼ�Σ����������Գ����ģ�
�⣺��1����ͼ��ʾ��

��2��ͼ��A����С��ת����60�����������ĶԳ�ͼ�Σ�
ͼ��B����С��ת����72�������������ĶԳ�ͼ�Σ�
ͼ��C����С��ת����72�������������ĶԳ�ͼ�Σ�
ͼ��D����С��ת����120�������������ĶԳ�ͼ�Σ�
ͼ��E����С��ת����90�����������ĶԳ�ͼ�Σ�
�ʴ�Ϊ��60���ǣ�72�����ǣ�72�����ǣ�120�����ǣ�90���ǣ�

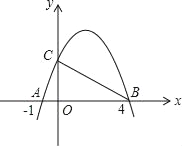
����Ŀ�����κ���y=ax2+bx+c��a��b��cΪ������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
x | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ��3 | ��4 | ��3 | 0 | 5 | 12 |
�����˽��ۣ�
��1�����κ���y=ax2+bx+c����Сֵ����СֵΪ��3��
��2������![]() ��x��2ʱ��y��0��
��x��2ʱ��y��0��
��3��a��b+c=0��
��4�����κ���y=ax2+bx+c��ͼ����x�����������㣬�����Ƿֱ���y������
��������ȷ���۵ĸ����ǣ�������
A. 1 B. 2 C. 3 D. 4