题目内容
6、已知：如图，Rt△ABC中，∠BAC=90°，D是AC上一点，∠ABD=∠C，直线EF过点D，与BA的延长线相交于F，且EF⊥BC，垂足为E．则图中所有与△ABD相似的三角形有多少个（ ）分析：根据两角对应相等，两三角形相似判断．
解答：解：∵∠BAC=90°，EF⊥BC，
∴∠BAC=∠BAD=∠CDE=90°，
∵∠ABD=∠C，
∴△ABD∽△ACB，△ABD∽△EDC（两角对应相等，两三角形相似）
∴∠ADB=∠ABC，
∴△ABD∽△EFB，
且△ABD∽△AFD
故选B．
∴∠BAC=∠BAD=∠CDE=90°，
∵∠ABD=∠C，
∴△ABD∽△ACB，△ABD∽△EDC（两角对应相等，两三角形相似）
∴∠ADB=∠ABC，
∴△ABD∽△EFB，
且△ABD∽△AFD
故选B．
点评：此题主要考查相似三角形的判定：两角对应相等，两三角形相似．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
22、已知：如图，Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°，试以图中标有字母的点为端点，连接两条线段，如果你所连接的两条线段满足相等，垂直或平行关系中的一种，那么请你把它写出来并证明．
20、已知：如图，Rt△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点，且不与A、B两点重合，AE⊥AB，AE=BD，连接DE、DC．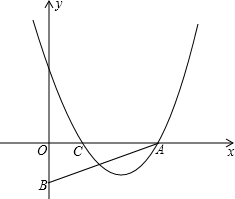
C=OB，抛物线y=（x-2）（x-m）-（p-2）（p-m）（m、p为常数且m+2≥2p＞0）经过A、C两点．
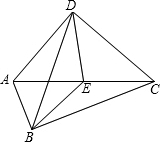已知：如图，Rt△ABC和Rt△ADC，∠ABC=∠ADC=90°，点E是AC的中点．
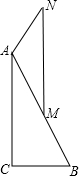已知：如图，Rt△ABC中，∠C=90°，M是AB的中点，AM=AN，MN∥AC．