题目内容
抛物线y=x2+2x-3与x轴交于A、B两点，与y轴交于C，则下列叙述不正确的是（ ）A．函数y有最小值-4
B．抛物线开口向上
C．△ABC面积是6
D．抛物线对称轴是直线x=1
【答案】分析：把抛物线的一般式表示为顶点式，交点式，可以知道抛物线的一些性质，再根据这些性质进行判断．
解答：解：∵抛物线y=x2+2x-3=（x+1）2-4=（x+3）（x-1），
∴顶点坐标为（-1，-4），对称轴是x=-1，开口向上，最小值是-4，
与x轴交点为（1，0），（-3，0），S△ABC=
×4×3=6．
故选D．
点评：主要考查了二次函数的性质和图象与坐标轴围成的图形面积求法．
解答：解：∵抛物线y=x2+2x-3=（x+1）2-4=（x+3）（x-1），
∴顶点坐标为（-1，-4），对称轴是x=-1，开口向上，最小值是-4，
与x轴交点为（1，0），（-3，0），S△ABC=
×4×3=6．故选D．
点评：主要考查了二次函数的性质和图象与坐标轴围成的图形面积求法．
练习册系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是（ ）
| A、（2，-2） | B、（1，-2） | C、（1，-3） | D、（-1，-3） |
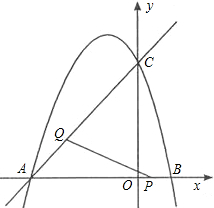秒，请求出△APQ的面积S与t的函数关系式，并求出当t为何值时，△APQ的面积最大，最大面积是多少？