题目内容
| 2x2+6x+4 |
| x2+3x+7 |
考点:二次函数的最值
专题:
分析:将
化为2-
后求得分母的最小值后即可求得原式的最小值.
| 2x2+6x+4 |
| x2+3x+7 |
| 10 |
| x2+3x+7 |
解答:解:
=2
=2-
,
x2+3x+7=(x+
)2+
,
∵x2+3x+7=(x+
)2+
,
∴x2+3x+7有最小值
,
∴
的最小值为2-
=-
,
故答案为:-
.
| 2x2+6x+4 |
| x2+3x+7 |
| x2+3x+7-5 |
| x2+3x+7 |
| 10 |
| x2+3x+7 |
x2+3x+7=(x+
| 3 |
| 2 |
| 19 |
| 4 |
∵x2+3x+7=(x+
| 3 |
| 2 |
| 19 |
| 4 |
∴x2+3x+7有最小值
| 19 |
| 4 |
∴
| 2x2+6x+4 |
| x2+3x+7 |
| 10 | ||
|
| 2 |
| 19 |
故答案为:-
| 2 |
| 19 |
点评:本题考查了二次函数的最值,对原式进行正确的变形是解答本题的关键.

练习册系列答案
相关题目
 如图,天平两边盘中标有相同字母的物体的质量相同,若A物体的质量为20克,当天平处于平衡状态时,B物体的质量为( )
如图,天平两边盘中标有相同字母的物体的质量相同,若A物体的质量为20克,当天平处于平衡状态时,B物体的质量为( )| A、5克 | B、10克 |
| C、15克 | D、30克 |
 如图,在△ABC中,AB=AC,D、E分别是AC,AB上的点,且BD=BC,BE=ED=AD,求∠A的度数.
如图,在△ABC中,AB=AC,D、E分别是AC,AB上的点,且BD=BC,BE=ED=AD,求∠A的度数.
 已知点A、B在反比例函数y=
已知点A、B在反比例函数y=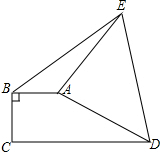 如图,直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,将腰DA以A为旋转中心逆时针旋转90°至AE,连接BE,DE,△ABE的面积为3,则CD的长为
如图,直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,将腰DA以A为旋转中心逆时针旋转90°至AE,连接BE,DE,△ABE的面积为3,则CD的长为