题目内容

如图，四边形ABCD的两条对角线AC，BD互相垂直，AC+BD=20，设AC的长度为x（cm），这个四边形的面积S（cm²）随x的变化而变化．
（1）请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）求当x为何值时，这个四边形ABCD的面积最大？最大面积是多少？
（参考公式：二次函数y=ax²+bx+c（a≠0），当x= $数学公式$ 时， $数学公式$ ）

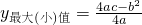解：（1）设AC的长度为x，
则BD=20-x，
∴S= $\text{[math]}$ AC×BD= $\text{[math]}$ x（20-x）=- $\text{[math]}$ x²+10x；

（2）S=- $\text{[math]}$ x²+10x=- $\text{[math]}$ （x-10）²+50，
∵- $\text{[math]}$ ＜0，
∴开口向下，
则当x=10时，S有最大值50
答：当x为10cm时，这个四边形ABCD的面积最大，最大面积是50（cm²）．
分析：（1）根据四边形面积= $\text{[math]}$ AC×BD，可得S= $\text{[math]}$ x（20-x）；
（2）利用配方法求出最大值即可．
点评：本题考查了二次函数的应用，难度一般，解答本题的关键是根据题意列出函数关系式并掌握利用配方法求最大值．