题目内容
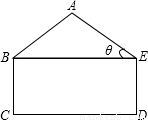
某工厂接受一批支援四川省汶川灾区抗震救灾账篷的生产任务．根据要求，账篷的一个横截面框架由等腰三角形和矩形组成（如图所示）．已知等腰三角形ABE的底角∠AEB=θ，且tanθ=| 3 | 4 |
分析：作AH⊥CD，垂足为H，交EB于点F，相等线段有AB=AE，BE=CD，BC=DE，且CD=2BC，再根据tanθ=
，可设AF=3x，EF=4x，AB、BE、CD的长就都可用x表示出来，由所用的钢管总长为17m所以可列方程，从而求出x，进而求出AH的长．
| 3 |
| 4 |
解答：
解：作AH⊥CD，垂足为H，交EB于点F，由矩形BCDE，得AH⊥BE．
∵△ABE是等腰三角形，CD=2BC，
∴点F为EB中点，EF=BF=BC=DE，
∵tanθ=
，
∴
=
，
设AF=3x，则EF=4x．
∴AE=5x，BE=8x，
∴BC=4x，
∴AB+BC+CD+DE+AE+BE=5x+4x+8x+4x+5x+8x=17，
∴x=0.5m，
∴AH=7x=7×0.5=3.5（m）．
答：篷顶A到底部CD的距离约为3.5m．
解：作AH⊥CD，垂足为H，交EB于点F，由矩形BCDE，得AH⊥BE．∵△ABE是等腰三角形，CD=2BC，
∴点F为EB中点，EF=BF=BC=DE，
∵tanθ=
| 3 |
| 4 |
∴
| AF |
| EF |
| 3 |
| 4 |
设AF=3x，则EF=4x．
∴AE=5x，BE=8x，
∴BC=4x，
∴AB+BC+CD+DE+AE+BE=5x+4x+8x+4x+5x+8x=17，
∴x=0.5m，
∴AH=7x=7×0.5=3.5（m）．
答：篷顶A到底部CD的距离约为3.5m．
点评：本题考查的是直角三角形的应用，解此题的关键是把实际问题转化为数学问题，要把实际问题抽象到直角三角形中，利用三角函数求解
练习册系列答案
相关题目
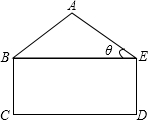某工厂接受一批支援四川省汶川灾区抗震救灾帐篷的生产任务．根据要求，帐篷的一个横截面框架由等腰三角形和矩形组成（如图所示）．已知等腰△ABE的底角∠AEB=θ，且tanθ=
，矩形BCDE的边CD=2BC，这个横截面框架（包括BE）所用的钢管总长为15m．求帐篷的篷顶A到底部CD的距离．（结果精确到0.1m）
，矩形BCDE的边CD=2BC，这个横截面框架（包括BE）所用的钢管总长为15m．求帐篷的篷顶A到底部CD的距离．（结果精确到0.1m）
，矩形BCDE的边CD=2BC，这个横截面框架（包括BE）所用的钢管总长为15m，求帐篷的篷顶A到底部CD的距离．（结果精确到0.1m）