题目内容
如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.


(1)求∠AOC的度数;
(2)在图(1)中,P为直径BA的延长线上一点,且 ,求证:PC为⊙O的切线.
,求证:PC为⊙O的切线.
(3)如图(2),一动点M从A点出发,在⊙O上按逆时针方向运动一周(点M不与点C重合),当 时,求动点M所经过的弧长.
时,求动点M所经过的弧长.
(1)60°; (2)证明见解析; (3) 或
或 或
或 或
或 .
.
【解析】
试题分析:(1)由OA、OC都是⊙O的半径知,△AOC是等腰三角形,然后根据等边三角形的判定和性质求得∠AOC =60°;
(2)由 求出PA的长,从而得出∠P=∠PCA,∠AOC=∠ACO,根据等边对等角和三角形内角和定理可得∠PCO=900,进而证得结论;
求出PA的长,从而得出∠P=∠PCA,∠AOC=∠ACO,根据等边对等角和三角形内角和定理可得∠PCO=900,进而证得结论;
(3)如图,当S△MAO=S△CAO时,动点M的位置有四种:①作点C关于直径AB的对称点M1,连接AM1,OM1,②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长.
试题解析:(1)在△OAC中,∵OA=OC(⊙O的半径),∠OAC=60°,∴∠OAC=∠OCA(等边对等角).
又∵∠OAC=60°,∴△AOC是等边三角形. ∴∠AOC=60°.
(2)如图,作PA边上的高CE,
∵△AOC是等边三角形, OC=4,∴CE= .
.
∵ ,∴
,∴ . ∴
. ∴ .∴PA=AC=AO=4. ∴
∠P=∠PCA,∠AOC=∠ACO.
.∴PA=AC=AO=4. ∴
∠P=∠PCA,∠AOC=∠ACO.
∴∠PCO=900.
又∵OC是⊙O的半径,∴PC为⊙O的切线.

(3)如图,
①作点C关于直径AB的对称点M1,连接AM1,OM1.
此时S△M1AO=S△CAO,∠AOM1=60°.∴弧AM1= .
.
∴当点M运动到M1时,S△MAO=S△CAO,此时点M经过的弧长为 .
.
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,
此时S△M2AO=S△CAO.∴∠AOM1=∠M1OM2=∠BOM2=60°.∴弧AM2= .
.
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为 .
.
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,
此时S△M3AO=S△CAO, ∴∠BOM3=60°.∴弧AM3= .
.
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为 .
.
点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为 .
.

考点:1.动点问题;2.等腰三角形的性质;3. 等边三角形的判定和性质;4.切线的判定;5. 弧长的计算;6.分类思想的应用.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案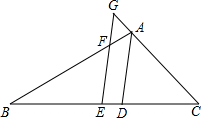 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.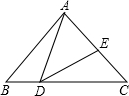 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.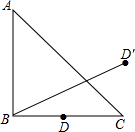 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=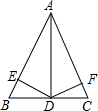 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有