题目内容
【题目】【问题背景】
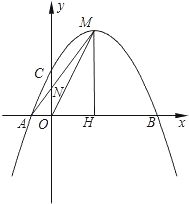
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
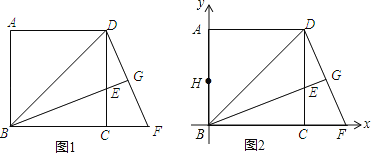
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

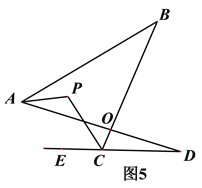
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
【答案】(1)理由见解析;
(2)∠P=26°;
∠P=![]() α+
α+![]() β;
β;![]()
【解析】(1)在△AOB中,∠A+∠B+∠AOB=180°,
在△COD中,∠C+∠D+∠COD=180°,
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;

(2)如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
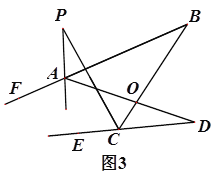
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,
∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=![]() (∠B+∠D)=
(∠B+∠D)=![]() ×(36°+16°)=26°;
×(36°+16°)=26°;
【拓展延伸】
∠P=![]() α+
α+![]() β
β
![]()

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目