题目内容
 如图,△ABC中,中线BD,CE相交于O.F、G分别为BO,CO的中点.
如图,△ABC中,中线BD,CE相交于O.F、G分别为BO,CO的中点.
(1)求证:四边形EFGD是平行四边形;
(2)若△ABC的面积为12,求四边形EFGD的面积.
(1)证明:∵BD,CE是△ABC的中线.
F,G分别为BO,CO的中点.
∴ED,FG分别为△ABC,△OBC的中位线
∴ED∥BC,ED= BC;
BC;
FG∥BC,FG= BC
BC
∴ED∥FG,ED=FG
∴四边形EFGD是平行四边形.
(2)解:∵DE,BD分别是△ABD,△ABC的中线.
如图,∴S△BDE= S△ABD=
S△ABD= S△ABC=
S△ABC= =3
=3
∵四边形EFGD是平行四边形,F为BO的中点.
∴OD=OF=BF,OE=OG
∴S△EBF=S△EFO=S△EOD= S△BDE=
S△BDE= =1,
=1,
S△GOF=S△GDO=S△EFO=S△EDO=1
∴S平行四边形EFGD=4S△EFO=4
故答案为四边形EFGD的面积为4.
分析:(1)本题利用了三角形的中位线来证明四边形EFGD的两对边分别平行即可;
(2)本题利用分解法将四边形EFGD分为四个三角形求出各自面积相加即可.
点评:本题主要考查了学生对三角形中位线定理、平行四边形性质及定理等方面的理解.
F,G分别为BO,CO的中点.
∴ED,FG分别为△ABC,△OBC的中位线
∴ED∥BC,ED=
 BC;
BC;FG∥BC,FG=
 BC
BC∴ED∥FG,ED=FG
∴四边形EFGD是平行四边形.
(2)解:∵DE,BD分别是△ABD,△ABC的中线.
如图,∴S△BDE=
 S△ABD=
S△ABD= S△ABC=
S△ABC= =3
=3∵四边形EFGD是平行四边形,F为BO的中点.
∴OD=OF=BF,OE=OG
∴S△EBF=S△EFO=S△EOD=
 S△BDE=
S△BDE= =1,
=1,S△GOF=S△GDO=S△EFO=S△EDO=1
∴S平行四边形EFGD=4S△EFO=4
故答案为四边形EFGD的面积为4.
分析:(1)本题利用了三角形的中位线来证明四边形EFGD的两对边分别平行即可;
(2)本题利用分解法将四边形EFGD分为四个三角形求出各自面积相加即可.
点评:本题主要考查了学生对三角形中位线定理、平行四边形性质及定理等方面的理解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 17、如图,△ABC中,∠1=∠2,∠EDC=∠BAC,AE=AF,∠B=60°,则图中的线段AF、BF、AE、EC、AD、BD、DC、DF中与DE的长相等的线段有
17、如图,△ABC中,∠1=∠2,∠EDC=∠BAC,AE=AF,∠B=60°,则图中的线段AF、BF、AE、EC、AD、BD、DC、DF中与DE的长相等的线段有 为圆心,半径为1cm的圆与AB相切,点E为切点.
为圆心,半径为1cm的圆与AB相切,点E为切点. 已知:如图,△ABC中,D、E、F、G均为BC边上的点,且BD=CG,DE=GF=
已知:如图,△ABC中,D、E、F、G均为BC边上的点,且BD=CG,DE=GF=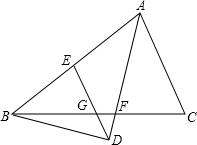 如图,△ABC中,BA=BC,∠C=72°,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,则图中的等腰三角形共有( ) 个.
如图,△ABC中,BA=BC,∠C=72°,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,则图中的等腰三角形共有( ) 个.