题目内容

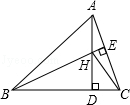
如图，△ABC中，∠B=，∠C=，AE是△ABC的角平分线，AD是BC上的高.求∠EAD的度数.
70°

试题分析：先根据三角形的内角和定理求得的度数，再根据角平分线的性质求得的度数，再由AD是BC上的高可得，最后根据三角形的内角和定理即可求得结果.
∠B=，∠C=

 AE是△ABC的角平分线

AD是BC上的高


°.
点评：解题的关键是熟练掌握角的平分线把角分成相等的两个小角，且都等于大角的一半.
练习册系列答案
相关题目
在五边形ABCDE中，∠A=100°, ∠B=∠C=112°, ∠D=108°则∠E=____°
以下列各组数据为边长作三角形，其中能组成直角三角形的是(      )
A．2，3，4 B．3，5，7
C．4，6，8D．6，8，10
已知：E是AB、CD外一点，∠D=∠B+∠E，求证：AB∥CD．
如图，在△ABC中，∠ACB=60°，∠BAC=75°，AD⊥BC于D，BE⊥AC于E，AD与BE交于H，则∠CHD=　 　．
如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，求证DF∥AC.

证明：∵∠1=∠2（已知）
∠2=∠3，∠1="∠4" （            ）
∴∠3=∠4 （     等量代换        ）
∴_____∥_____ (                                  )
∴∠C=∠ABD  (                                  )
∵∠C=∠D    (   已知      )
∴∠D=∠ABD   (     等量代换       )
∴DF∥AC
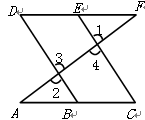
如图，在△ABC中，已知点D，E，F分别是BC、AD、CE的中点，且＝4cm2，则的值为（    ）

A.2cm2     B.1cm2        C.cm2         D.cm2
如图，如果△ABC≌△DEF，△DEF周长是32cm，DE=9cm，EF=13cm，∠E=∠B，则AC=　 　cm．
一副三角板如图摆放，若∠AGB=90°，则∠AFE=__________度。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网