题目内容
计算:
(1)若 +|n+2|=0,试求mn的立方根.
+|n+2|=0,试求mn的立方根.
(2) +
+ -
-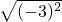 .
.
解:(1)∵ +|n+2|=0,
+|n+2|=0,
∴m-4=0,n+2=0,
∴m=4,n=-2.
则mn=4×(-2)=-8,
∴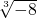 =-2.
=-2.
(2)原式= +
+ -3
-3
= +
+ -3
-3
=
= .
.
分析:(1)根据非负数的性质求出m、n的值,再代入mn,然后求出其立方根;
(2)将被开方数化为假分数,再开方.
点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握非负数的性质、二次根式的化简等考点的运算.
 +|n+2|=0,
+|n+2|=0,∴m-4=0,n+2=0,
∴m=4,n=-2.
则mn=4×(-2)=-8,
∴
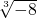 =-2.
=-2.(2)原式=
 +
+ -3
-3=
 +
+ -3
-3=

=
 .
.分析:(1)根据非负数的性质求出m、n的值,再代入mn,然后求出其立方根;
(2)将被开方数化为假分数,再开方.
点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握非负数的性质、二次根式的化简等考点的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目