题目内容
已知:二次函数y=x2+2x+a(a为大于0的常数),当x=m时的函数值y1<0;则当x=m+1时的函数值y2与0的大小关系为
- A.y2>0
- B.y2<0
- C.y2=0
- D.不能确定
A
分析:根据抛物线与x轴的交点情况,判断a的取值范围,即0<a<1,已知对称轴是x=-1,则-2<m<0,0<m+1<2,可判断当x=m+1时,函数值y2与0的大小关系为y2>0.
解答:∵抛物线与x轴有两个交点,
∴△=22-4a>0,即a<1,
又∵a>0,对称轴为x=-1,
∴-1-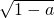 <x<-1+
<x<-1+ 时,y<0,
时,y<0,
∵当x=m时的函数值y1<0,
故-1-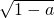 <m<-1+
<m<-1+
则当x=m+1时,函数值y2与0的大小关系为y2>0.
故选A.
点评:本题主要考查二次函数的性质的知识点,解答本题的关键是熟练掌握二次函数的图象与性质,此题难度不大,还可以进行数形结合进行解答.
分析:根据抛物线与x轴的交点情况,判断a的取值范围,即0<a<1,已知对称轴是x=-1,则-2<m<0,0<m+1<2,可判断当x=m+1时,函数值y2与0的大小关系为y2>0.
解答:∵抛物线与x轴有两个交点,
∴△=22-4a>0,即a<1,
又∵a>0,对称轴为x=-1,
∴-1-
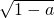 <x<-1+
<x<-1+ 时,y<0,
时,y<0,∵当x=m时的函数值y1<0,
故-1-
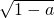 <m<-1+
<m<-1+
则当x=m+1时,函数值y2与0的大小关系为y2>0.
故选A.
点评:本题主要考查二次函数的性质的知识点,解答本题的关键是熟练掌握二次函数的图象与性质,此题难度不大,还可以进行数形结合进行解答.

练习册系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.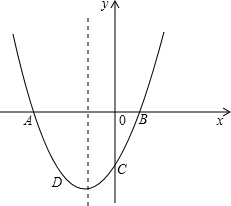 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.