Question

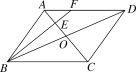
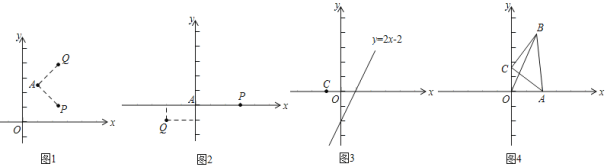
【题目】对于平面直角坐标系xOy中的点A和点P，若将点P绕点A逆时针旋转90°后得到点Q，则称点Q为点P关于点A的“垂链点”，图1为点P关于点A的“垂链点”Q的示意图．

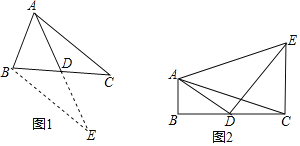
（1）如图2，已知点A的坐标为（0，0），点P关于点A的“垂链点”为点Q；

①若点P的坐标为（3，0），则点Q的坐标为　 　；

②若点Q的坐标为（﹣2，﹣1），则点P的坐标为　 　；

（2）如图3，已知点C的坐标为（﹣1，0），点D在直线y＝2x﹣2上，若点D关于点C的“垂链点”E在坐标轴上，试求出点D的坐标；

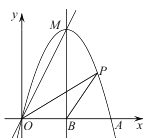
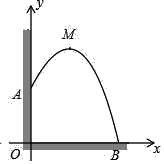
（3）如图4，在平面直角坐标系xOy，已知点A（2，0），点C是y轴上的动点，点A关于点C的“垂链点”是点B，连接BO、BA，则BO+BA的最小值是　 　．

Answer 1

【答案】（1）①（0，3）；②（﹣1，2）；（2）点D（﹣1，﹣4）或（，﹣1）；（3）．

【解析】

（1）①若点P的坐标为（3，0），则点Q的坐标为 （0，3），②若点Q的坐标为（﹣2，﹣1），同理可得：点P的坐标为（﹣1，2）；

（2）分当点E（E′）落在x轴上、点E落在y轴两种情况，分别求解即可；

（3）BO+BA＝

，BO+BA的值，相当于求点P（m，m）到点M（1，﹣1）和点N（0，﹣1）的最小值，相当于在直线y＝x上寻找一点P（m，m），使得点P到M（0，﹣1），到N（1，﹣1）的距离和最小，即可求解．

解：（1）①若点P的坐标为（3，0），则点Q的坐标为 （0，3），

故答案为：（0，3）；

②若点Q的坐标为（﹣2，﹣1），

同理可得：点P的坐标为（﹣1，2），

故答案为：（﹣1，2）；

（2）①当点E（E′）落在x轴上时，如图1

则点D（D′）关于点C的“垂链点”在x轴上，点CD⊥x轴，

x＝﹣1时，y＝﹣2﹣2＝﹣4，

故点D（﹣1，﹣4）；

②当点E落在y轴时，如图1：

设点D（m，2m﹣2），

点D的“垂链点E在y轴上，

过点D作DH⊥x轴于点H，

则△CHD≌△EOC（AAS），

则DH＝OC＝1，即：2m﹣2＝﹣1，解得：m＝，

故点D（，﹣1），

综上，点D（﹣1，﹣4）或（，﹣1）；

（3）如图作BH⊥OH于H．

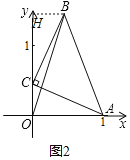
设点C的坐标为（0，m），

由（1）知：OC＝HB＝m，OA＝HC＝1，

则点B（m，1+m），

则：BO+BA＝

，

BO+BA的值，相当于求点P（m，m）到点M（1，﹣1）和点N（0，﹣1）的最小值，

相当于在直线y＝x上寻找一点P（m，m），使得点P到M（0，﹣1），到N（1，﹣1）的距离和最小，

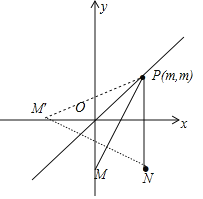
作M关于直线y＝x的对称点M′（﹣1，0），

易知PM+PN＝PM′+PN≥NM′，

M′N＝＝，

故答案为：．