题目内容
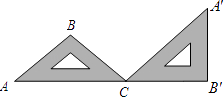
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1 , l2 , l3上,且l1 , l2之间的距离为2,l2 , l3之间的距离为3,则AC的长是( ) 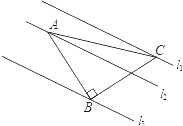
A.![]()
B.![]()
C.![]()
D.7
【答案】A
【解析】解:作AD⊥l3于D,作CE⊥l3于E, 
∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE, ,
,
∴△ABD≌△BCE
∴BE=AD=3
在Rt△BCE中,根据勾股定理,得BC= ![]() =
= ![]() ,
,
在Rt△ABC中,根据勾股定理,得AC= ![]() ×
× ![]() =2
=2 ![]() ;
;
故选A.
过A、C点作l3的垂线构造出直角三角形,根据三角形全等和勾股定理求出BC的长,再利用勾股定理即可求出.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目