题目内容
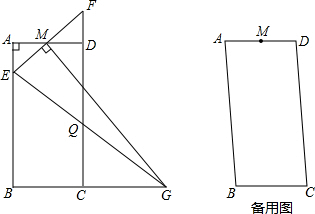
（2011•虹口区模拟）如图，用线段AB表示的高楼与地面垂直，在高楼前D点测得楼顶A的仰角为30°，向高楼前进60米到C点，又测得楼顶A的仰角为45°，且D、C、B三
点在同一直线上，则该高楼的高度为
点在同一直线上，则该高楼的高度为（30
+30）
| 3 |
（30
+30）
米（结果保留根号）．| 3 |
分析：由于AB是Rt△ABD和Rt△ABC的公共直角边，可在Rt△ABC中，根据∠ACB的正切值，用AB表示出BC的长；同理可在Rt△ABD中，根据∠D的度数，用AB表示出BD的长；根据CD=BD-BC，即可求得AB的长．
解答：解：Rt△ABC中，∠ACB=45°，
∴BC=AB；
Rt△ABD中，∠ADB=30°，
∴BD=
=
AB；
∴DC=BD-BC=（
-1）AB=60米．
∴AB=
=（30
+30）米．
答：楼的高度为（30
+30）米．
∴BC=AB；
Rt△ABD中，∠ADB=30°，
∴BD=
| AB |
| tan30° |
| 3 |
∴DC=BD-BC=（
| 3 |
∴AB=
| 60 | ||
|
| 3 |
答：楼的高度为（30
| 3 |
点评：本题考查仰角的定义，以及解直角三角形的实际应用问题．此题难度不大，解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形，注意当两个直角三角形有公共边时，利用这条公共边进行求解是解此类题的常用方法．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
（2011•虹口区一模）已知抛物线y=ax2+bx+c（a≠0）如图所示，下列结论中，正确的是（ ）
（2011•虹口区一模）如图，在3×4的方格上，每个方格的边长为1个单位，△ABC的顶点都在方格的格点位置．若点D在格点位置上（与点A不重合），且使△DBC与△ABC相似，则符合条件的点D共有
