题目内容
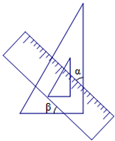将一个直角三角板和一把直尺如图放置，如果∠α=43°，则∠β的度数是________．
47°
分析：首先过点C作CH∥DE交AB于H，即可得CH∥DE∥FG，然后利用两直线平行，同位角相等与余角的性质，即可求得∠β的度数．
解答：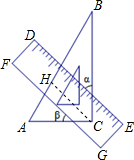
解：如图，根据题意得：∠ACB=90°，DE∥FG，
过点C作CH∥DE交AB于H，
∴CH∥DE∥FG，
∴∠BCH=∠α=43°，
∴∠HCA=90°-∠BCH=47°，
∴∠β=∠HCA=47°．
故答案为：47°．
点评：此题考查了平行线的性质．此题难度不大，解题的关键是准确作出辅助线，掌握两直线平行，同位角相等定理的应用．
分析：首先过点C作CH∥DE交AB于H，即可得CH∥DE∥FG，然后利用两直线平行，同位角相等与余角的性质，即可求得∠β的度数．
解答：
解：如图，根据题意得：∠ACB=90°，DE∥FG，过点C作CH∥DE交AB于H，
∴CH∥DE∥FG，
∴∠BCH=∠α=43°，
∴∠HCA=90°-∠BCH=47°，
∴∠β=∠HCA=47°．
故答案为：47°．
点评：此题考查了平行线的性质．此题难度不大，解题的关键是准确作出辅助线，掌握两直线平行，同位角相等定理的应用．
练习册系列答案
相关题目
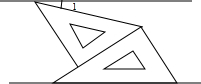（2013•盘锦）如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（ ）
（2012•如东县一模）将一个直角三角板和一把矩形直尺按如图放置，若∠α=55°，则∠β的度数是
