题目内容
如图，⊙O的直径为AB，周长为P1，在⊙O内的n个圆心在AB上且依次相外切的等圆，且其中左、右两侧的等圆分别与⊙O内切于A、B，若这n个等圆的周长之和为P2，则P1和P2的大小关系是（ ）| A、P1＜P2 | B、P1=P2 | C、P1＞P2 | D、不能确定 |
分析：由题意可分别求出P1、P2关于AB的表达式，比较二者大小即可求得P1、P2大小关系．
解答：解：∵⊙O的直径为AB，周长为P1
∴P1=2π×
=π•AB．
∵⊙O内的n个圆心在AB上且依次相外切的等圆，
∴n个小圆的半径为
，
∴P2=2π×
×n=π•AB，
∴P1=P2．
故选B．
∴P1=2π×
| AB |
| 2 |
∵⊙O内的n个圆心在AB上且依次相外切的等圆，
∴n个小圆的半径为
| AB |
| 2n |
∴P2=2π×
| AB |
| 2n |
∴P1=P2．
故选B．
点评：本题主要考查了相切圆的性质．
练习册系列答案
相关题目
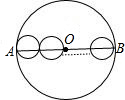如图，⊙O的直径为AB，周长为P1，在⊙O内的n个圆心在AB上且依次相外切的等圆，且其中左、右两侧的等圆分别与⊙O内切于A、B，若这n个等圆的周长之和为P2，则P1和P2的大小关系是（ ）| A、P1＜P2 | B、P1=P2 | C、P1＞P2 | D、不能确定 |
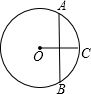如图，⊙O的直径为10 cm，弦AB垂直平分半径OC，则弦AB长为（ ）| A、2.5cm | ||
| B、5cm | ||
C、5
| ||
| D、10cm |
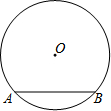（2013•南京二模）如图，⊙O的直径为10，弦AB的长为8，则点O到AB的距离为
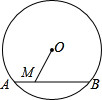如图，⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，则OM的长的取值范围是
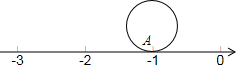如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示-1的点重合，将圆沿数轴滚动1周，点A到达点A′的位置，则点A′表示的数是