题目内容
 已知Rt△OAB在直角坐标系中的位置如图所示,点P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,若分割得到的三角形与Rt△OAB相似,则点C的坐标为
已知Rt△OAB在直角坐标系中的位置如图所示,点P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,若分割得到的三角形与Rt△OAB相似,则点C的坐标为(3,0)或(6,4)或(6,
)
| 7 |
| 4 |
(3,0)或(6,4)或(6,
)
.| 7 |
| 4 |
分析:根据平行于三角形一边的直线分成的三角形与原三角形相似,可得PC∥AB,PC∥OA时,分割得到的三角形与Rt△OAB相似,根据网格结构写出此时点C的坐标即可;又当PC⊥OB时,分割得到的三角形与Rt△OAB也相似,根据网格结构,利用勾股定理求出OB的长度,然后根据相似三角形对应边成比例列式求出分割得到的三角形的斜边的长度,然后判定点C在AB上,再求出AC的长度,从而得到此时点C的坐标.
解答: 解:如图,①PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0);
解:如图,①PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0);
②PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4);
③PC⊥OB时,设分割得到的三角形的斜边的长为x,
根据勾股定理得,OB=10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴
=
,
解得x=
,
∵
>6,
∴点C在边AB上,
∴AC=8-
=
,
此时,点C的坐标为(6,
);
综上所述,点C的坐标为(3,0)或(6,4)或(6,
).
故答案为:(3,0)或(6,4)或(6,
).
 解:如图,①PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0);
解:如图,①PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0);②PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4);
③PC⊥OB时,设分割得到的三角形的斜边的长为x,
根据勾股定理得,OB=10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴
| x |
| 10 |
| 5 |
| 8 |
解得x=
| 25 |
| 4 |
∵
| 25 |
| 4 |
∴点C在边AB上,
∴AC=8-
| 25 |
| 4 |
| 7 |
| 4 |
此时,点C的坐标为(6,
| 7 |
| 4 |
综上所述,点C的坐标为(3,0)或(6,4)或(6,
| 7 |
| 4 |
故答案为:(3,0)或(6,4)或(6,
| 7 |
| 4 |
点评:本题考查了相似三角形的性质,坐标与图形的性质,熟练掌握相似三角形的判定方法是解题的关键,主要要分情况讨论求解.

练习册系列答案
相关题目
 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分. 已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.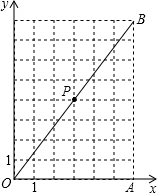 已知Rt△OAB在直角坐标系中的位置如图所示,点P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,若分割得到的三角形与Rt△OAB相似,则点C的坐标为________.
已知Rt△OAB在直角坐标系中的位置如图所示,点P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分,若分割得到的三角形与Rt△OAB相似,则点C的坐标为________.