题目内容
7. 如图,在菱形ABCD中,AB=13,对角线BD=24,若过点C作CE⊥AB,垂足为E,则CE的长为( )
如图,在菱形ABCD中,AB=13,对角线BD=24,若过点C作CE⊥AB,垂足为E,则CE的长为( )| A. | $\frac{120}{13}$ | B. | 10 | C. | 12 | D. | $\frac{240}{13}$ |
分析 连接AC交BD于O,由菱形的性质得出OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD=12,AC⊥BD,由勾股定理求出OA,得出AC,再由菱形面积的两种计算方法,即可求出CE的长.
解答 解:连接AC交BD于O,如图所示:
∵四边形ABCD是菱形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD=12,AC⊥BD,
∴∠AOB=90°,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{13}^{2}-1{2}^{2}}$=5,
∴AC=10,
∵菱形的面积=AB•CE=$\frac{1}{2}$AC•BD,
即13×CE=$\frac{1}{2}$×10×24,
解得:CE=$\frac{120}{13}$.
故选:A.
点评 本题考查了菱形的性质、勾股定理、菱形面积的计算方法;熟练掌握菱形的性质,由菱形面积的两种计算方法得出结果是解决问题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.下列说法中,正确的是( )
| A. | 希望小学初一年级的367名同学中,至少有两个生日相同的概率是1 | |
| B. | 在投掷骰子时,连投两次点数相同的概率与连投两次点数都为1的概率相等 | |
| C. | 我们小组共8名同学,他们中肯定有两人在同一月过生日 | |
| D. | 一个游戏的中奖率是1%,买100张奖券,一定会中奖 |
18.长方形的周长为c米,宽为x米,则长为( )
| A. | (c-2x)米 | B. | $\frac{c-2x}{2}$米 | C. | $\frac{c-x}{2}$米 | D. | $\frac{c}{2}$-2x米 |
2.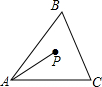 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
 如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )
如图所示,点P为△ABC三边垂直平分线的交点,PA=6,则点P到点C的距离为PC满足( )| A. | PC<6 | B. | PC=6 | C. | PC>6 | D. | 以上都不对 |
16.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2015的值为( )
| A. | -1005 | B. | -1006 | C. | -1007 | D. | -2014 |
 解不等式组$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{5-\frac{1}{2}x>2x}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{5-\frac{1}{2}x>2x}\end{array}\right.$,并把解集在数轴上表示出来.