题目内容
在平面直角坐标系中 ,已知椭圆
,已知椭圆 过点
过点 ,且椭圆
,且椭圆 的离心率为
的离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)是否存在以 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆 的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
的等腰直角三角形?若存在,求出共有几个;若不存在,请说明理由.
解:(1)由 得
得 , ……1分
, ……1分
又 . ……2分
. ……2分
故椭圆 方程为
方程为 ,
,
椭圆 经过点
经过点 ,则
,则 . ……3分
. ……3分
所以 ……4分
……4分
所以椭圆 的
的 标准方程为
标准方程为 . ……5分
. ……5分
(2)假设存在这样的等腰直角三角形 .
.
明显直线 的斜率存在,因为
的斜率存在,因为 点的坐标为
点的坐标为 ,设直线
,设直线 的方程
的方程 ,则直线
,则直线 的方程为
的方程为 . ……6分
. ……6分
由 得
得

所以 ,或
,或
所以 点的纵坐标为
点的纵坐标为 ……7分
……7分
所以 . ……8分
. ……8分
同理
 ……9分
……9分
因为 是等腰直角三角形,所以
是等腰直角三角形,所以 ,即
,即
 ……10分
……10分
即
所以 ,即
,即 ……11分
……11分
所以
即
所以 ,或
,或 ……12分
……12分
所以 ,或
,或 . ……13分
. ……13分
所以这样的直角三角形有三个.  ……14分
……14分

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案 , 则输出
, 则输出
 的值为
的值为 B.
B. C.
C. D.
D.

 与圆
与圆 ,则
,则 上各点到
上各点到 的距离的最小值为_____________.
的距离的最小值为_____________.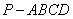 的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于
的底面边长为6cm,侧棱长为5cm,则它的正视图的面积等于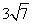 B.
B. 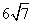 C.12 D.24
C.12 D.24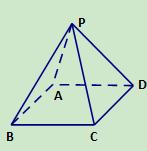

 =2的解为非负数,则m的取值范围是( )
=2的解为非负数,则m的取值范围是( ) ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y= 图象经过点A.
图象经过点A.