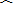题目内容
已知：如图△ABC中，∠A的平分线AD交BC于D，⊙O过点A，且与BC相切于D，与AB、AC分别相交于E、F，AD与EF相交于G．
（1）求证：AF•FC=GF•DC；
（2）已知AC=6cm，DC=2cm，求FC、GF的长．
（1）求证：AF•FC=GF•DC；
（2）已知AC=6cm，DC=2cm，求FC、GF的长．
（1）证明：连接DF，
∵AD是△ABC的角平分线，BC是⊙O的切线，∠CDF=∠EFD=∠DAC=∠EAD，
∴EF∥BC．
∴∠C=∠AFE．
∴△AFG∽△DCF，
∴
=
，
即AF•FC=GF•DC；
（2）∵BC是⊙O的切线，
∴CD2=CF•AC，
∵AC=6cm，DC=2cm，
∴CF=
，
∴AF=AC-CF=
∵△AFG∽△DCF，
∴
=
，
∴
=
，
∴GF=
．
∵AD是△ABC的角平分线，BC是⊙O的切线，∠CDF=∠EFD=∠DAC=∠EAD，
∴EF∥BC．
∴∠C=∠AFE．
∴△AFG∽△DCF，
∴
| AF |
| DC |
| GF |
| CF |
即AF•FC=GF•DC；
（2）∵BC是⊙O的切线，
∴CD2=CF•AC，
∵AC=6cm，DC=2cm，
∴CF=
| 2 |
| 3 |
∴AF=AC-CF=
| 16 |
| 3 |
∵△AFG∽△DCF，
∴
| AF |
| DC |
| GF |
| CF |
∴
| ||
| 2 |
| GF | ||
|
∴GF=
| 16 |
| 9 |
练习册系列答案
备战中考寒假系列答案
相关题目
