题目内容
 勾股定理反映的是如图1,∠C=90°时,S正方形ACED+S正方形BCLH=S正方形AGFB.猜想,如图2,BC为直径半圆的面积与AC为直径半圆的面积和是否等于AB为直径半圆的面积为什么?
勾股定理反映的是如图1,∠C=90°时,S正方形ACED+S正方形BCLH=S正方形AGFB.猜想,如图2,BC为直径半圆的面积与AC为直径半圆的面积和是否等于AB为直径半圆的面积为什么?
分析:此题主要还是利用的勾股定理,只不过这里,可把勾股定理和圆的面积公式结合起来,计算出圆的面积,两个小圆的面积相加正好是大圆的面积,所以相等.
解答:解:由勾股定理可知:AB2=BC2+AC2.
由圆的面积公式可知:三个半圆的面积分别是:
π(
)2,
π(
)2,
π(
)2.三者建立等式可得相等.
由圆的面积公式可知:三个半圆的面积分别是:
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 2 |
| AC |
| 2 |
点评:此题主要考查了圆的面积公式,在此题中要把勾股定理的结论当成一个条件来使用.这样才能使式子成立.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
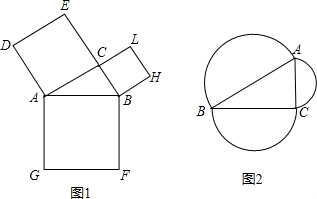 勾股定理反映的是如图1,∠C=90°时,S正方形ACED+S正方形BCLH=S正方形AGFB.猜想,如图2,BC为直径半圆的面积与AC为直径半圆的面积和是否等于AB为直径半圆的面积为什么?
勾股定理反映的是如图1,∠C=90°时,S正方形ACED+S正方形BCLH=S正方形AGFB.猜想,如图2,BC为直径半圆的面积与AC为直径半圆的面积和是否等于AB为直径半圆的面积为什么?