Question

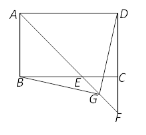
【题目】已知如图1，抛物线y=﹣x2﹣x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC

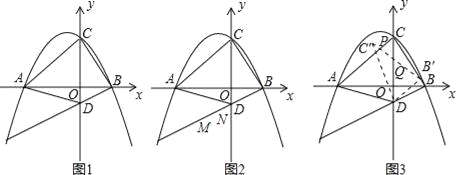
（1）求出直线AD的解析式；

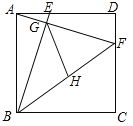
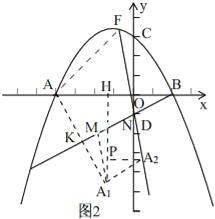
（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；

（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．

Answer 1

【答案】（1）直线AD解析式为y=﹣x﹣1；（2）N点的横坐标为：﹣;（3）PC的值为： 或4﹣或或．

【解析】解：（1）∵抛物线y=﹣x2﹣x+3与x轴交于A和B两点，

∴0=﹣x2﹣x+3，

∴x=2或x=﹣4，

∴A（﹣4，0），B（2，0），

∵D（0，﹣1），

∴直线AD解析式为y=﹣x﹣1；

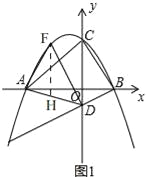
（2）如图1，

过点F作FH⊥x轴，交AD于H，

设F（m，﹣m2﹣m+3），H（m，﹣m﹣1），

∴FH=﹣m2﹣m+3﹣（﹣m﹣1）=﹣m2﹣m+4，

∴S△ADF=S△AFH+S△DFH=FH×|yD﹣yA|=2FH=2（﹣m2﹣m+4）=﹣m2﹣m+8=﹣（m+）2+，

当m=﹣时，S△ADF最大，

∴F（﹣，）

如图2，

作点A关于直线BD的对称点A1，把A1沿平行直线BD方向平移到A2，且A1A2=，

连接A2F，交直线BD于点N，把点N沿直线BD向左平移得点M，此时四边形AMNF的周长最小．

∵OB=2，OD=1，

∴tan∠OBD=，

∵AB=6，

∴AK=，

∴AA1=2AK=，

在Rt△ABK中，AH=，A1H=，

∴OH=OA﹣AH=，

∴A1（﹣，﹣），

过A2作A2P⊥A2H，

∴∠A1A2P=∠ABK，

∵A1A2=，

∴A2P=2，A1P=1，

∴A2（﹣，﹣）

∵F（﹣，）

∴A2F的解析式为y=﹣x﹣①，

∵B（2，0），D（0，﹣1），

∴直线BD解析式为y=﹣x﹣1②，

联立①②得，x=﹣，

∴N点的横坐标为：﹣．

（3）∵C（0，3），B（2，0），D（0，﹣1）

∴CD=4，BC=，OB=2，

BC边上的高为DH，

根据等面积法得，BC×DH=CD×OB，

∴DH==，

∵A（﹣4，0），C（0，3），

∴OA=4，OC=3，

∴tan∠ACD=，

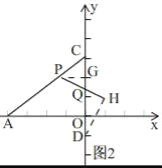
①当PC=PQ时，简图如图1，

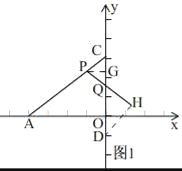
过点P作PG⊥CD，过点D作DH⊥PQ，

∵tan∠ACD=

∴设CG=3a，则QG=3a，PG=4a，PQ=PC=5a，

∴DQ=CD﹣CQ=4﹣6a

∵△PGQ∽△DHQ，

∴，

∴，

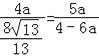
∴a=，

∴PC=5a=；

②当PC=CQ时，简图如图2，

过点P作PG⊥CD，

∵tan∠ACD=

∴设CG=3a，则PG=4a，

∴CQ=PC=5a，

∴QG=CQ﹣CG=2a，

∴PQ=2a，

∴DQ=CD﹣CQ=4﹣5a

∵△PGQ∽△DHQ，

同①的方法得出，PC=4﹣，

③当QC=PQ时，简图如图1

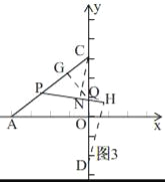
过点Q作QG⊥PC，过点C作CN⊥PQ，

设CG=3a，则QG=4a，PQ=CQ=5a，

∴PG=3a，

∴PC=6a

∴DQ=CD﹣CQ=4﹣5a，

利用等面积法得，CN×PQ=PC×QG，

∴CN=a，

∵△CQN∽△DQH

同①的方法得出PC=

④当PC=CQ时，简图如图4，

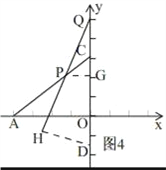
过点P作PG⊥CD，过H作HD⊥PQ，

设CG=3a，则PG=4a，CQ=PC=5a，

∴QD=4+5a，PQ=4，

∵△QPG∽△QDH，

同①方法得出．CP=

综上所述，PC的值为：；4﹣，，=．