��Ŀ����
����Ŀ�������⣺
��1������գ��������������������ɶ������涨����__________��
���ɶ������涨�����������ж�һ����������ֱ�������εķ�������ѧ����һЩ��������ͼ�ε��ж�������ͬ����ͨ���������жϣ�ʵ���ϼ����ڼ�����Ҳ�Ǻ���Ҫ�ģ�����ѧ������������Ͻ�������ѧϰ���ɶ������涨��������Ҫ������չ˼ά����һ�������ѧ�еĸ��ַ�����
��2�����Ķ���С����ѧϰ���ɶ������������ü���ķ���������֤��������������⣺
��ͼ![]() �У�
��![]() ��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ����˵�������߶�
����˵�������߶�![]() ��
��![]() ��
��![]() ���ܹ���һ��ֱ�������Σ�
���ܹ���һ��ֱ�������Σ�
֤������![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��ȥ![]() ����
����![]() ���Ӷ���
���Ӷ���![]() ��
��
����Ϊ��![]() �У�
��![]() ��
��
��ȥ![]() ��
��![]() ����ȥ
����ȥ![]() ������
������![]() ����
����![]() ��
��
���ԣ������߶�![]() ��
��![]() ��
��![]() ���ܹ���һ��ֱ�������Σ�
���ܹ���һ��ֱ�������Σ�
�ɼ��������ڼ���֤����Ҳ�Ǻ���Ҫ�ģ�С���������ô����м��㡢��Ԫ���ֶΣ������ض�������֤�˼������⣮
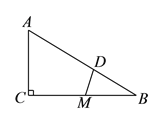
��3����������⣺�ھ���![]() �У���
����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() ��
��![]() ��
��![]() �ϣ�ʹ��
�ϣ�ʹ��![]() ����֤���ı���
����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
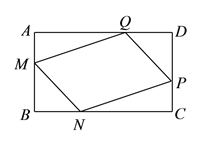
���𰸡�������
�����������������
��1���������������������ɶ������涨�����ɣ�
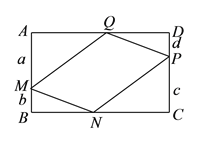
��3����ͼ����AM=a��BM=b��PC=c��PD=d�������֪�ɵã�![]() ��
��![]() ��
��![]() ��
��![]() �����ı���ABCD�Ǿ��οɵ�AB=CD��AD=BC�����г���������a��b��c��d�ĵ�ʽ���ѵ�ʽ���μ���֤��a=c��b=d���Ӷ��ɵ�AM=CP��BM=PD��AQ=CN��DQ=BN����֤��AMQ�ա�CPN����BMN�ա�DPQ������֤��MQ=PN��MN=PQ���Ӷ��ɵ��ı���MNPQ��ƽ���ı���.
�����ı���ABCD�Ǿ��οɵ�AB=CD��AD=BC�����г���������a��b��c��d�ĵ�ʽ���ѵ�ʽ���μ���֤��a=c��b=d���Ӷ��ɵ�AM=CP��BM=PD��AQ=CN��DQ=BN����֤��AMQ�ա�CPN����BMN�ա�DPQ������֤��MQ=PN��MN=PQ���Ӷ��ɵ��ı���MNPQ��ƽ���ı���.
���������
1�����ɶ������涨������Ϊ�����һ�������ε����߳�![]() ��
��![]() ��
��![]() ������
������![]() ��
��
��ô�����������ֱ�������Σ�
3����![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�� �ı���![]() Ϊ���Σ�
����
�� ![]() ��
��![]() ��
��
�� 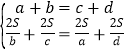 ��
��
�����ã�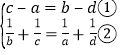 ��
��
�������ã�![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
�� ![]() ��
��
�� ![]() ����a=c��
����a=c��
�� b-d=c-a=0��
�� ![]() ��
��
�� AM=CP��BM=PD��AQ=CN��DQ=BN��
���ߡ�A=��B=��C=��D=90�㣬
���AMQ�ա�CPN����BMN�ա�DPQ��
�� ![]() ��
��![]() ��
��
�� �ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�








