Question

在平面直角坐标系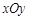中，抛物线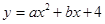经过A（－3,0）、B（4,0）两点，且与y轴交于点C，点D在x轴的负半轴上，且BD＝BC，有一动点P从点A出发，沿线段AB以每秒1个单位长度的速度向点B移动，同时另一个动点Q从点C出发，沿线段CA以某一速度向点A移动.

【小题1】求该抛物线的解析式；
【小题2】若经过t秒的移动，线段PQ被CD垂直平分，求此时t的值；
【小题3】该抛物线的对称轴上是否存在一点M，使MQ＋MA的值最小？若存在，求出点M的坐标；若不存在，请说明理由.

Answer 1

【小题1】∵抛物线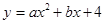经过A（－3,0），B（4,0）两点，
∴ 
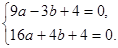
解得
∴所求抛物线的解析式为.
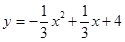【小题1】如图，依题意知AP＝t，连接DQ，

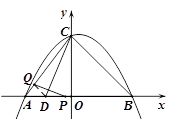
由A（－3,0），B（4,0），C（0,4），
可得AC＝5，BC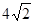＝，AB＝7.
∵BD＝BC，
∴.
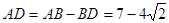∵CD垂直平分PQ，
∴QD＝DP，∠CDQ= ∠CDP.
∵BD＝BC，
∴∠DCB= ∠CDB.
∴∠CDQ= ∠DCB.
∴DQ∥BC. 
∴△ADQ∽△ABC.
∴.
∴.
∴.
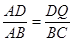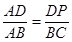解得 .
∴
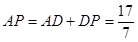
∴线段PQ被CD垂直平分时，t的值为.
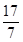【小题1】设抛物线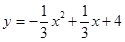的对称轴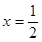与x轴交于点E.
点A、B关于对称轴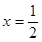对称，连接BQ交该对称轴于点M.

则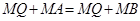，即.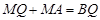
当BQ⊥AC时，BQ最小. 
此时，∠EBM= ∠ACO.
∴.
∴.
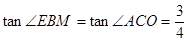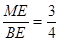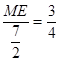∴，解得.
∴M（，）.
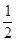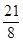即在抛物线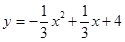的对称轴上存在一点M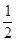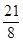（，），使得
MQ＋MA的值最小.解析:
【小题1】把A、B两点坐标代入求出抛物线的解析式；
【小题1】连接DQ，先求出△ADQ∽△ABC.得出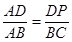，从而求出t的值；
【小题1】∵MQ+MA=BM，∴只需找到B点到AC的长度最短，即过B点作BQ⊥AC，BQ最短，然后求出BQ与对称轴的交点M的坐标。