题目内容
2.$\frac{1}{2}$x-2(x-$\frac{1}{3}$y2)+(-$\frac{2}{3}$x+$\frac{1}{3}$y2),其中x=-2,y=-$\frac{2}{3}$.分析 先化简,然后将x与y的值代入即可求出答案.
解答 解:原式=$\frac{1}{2}$x-2x+$\frac{2}{3}$y2-$\frac{3}{2}$x+$\frac{1}{3}$y2
=-3x+y2
当x=-2,y=-$\frac{2}{3}$时
∴原式=-3×(-2)+$\frac{4}{9}$=6$\frac{4}{9}$
点评 本题考查整式的加减,涉及代入求值,属于基础题型.

练习册系列答案
相关题目
18.下列各对数中,相等的一对数是( )
| A. | (-2)3与-23 | B. | -22与(-2)2 | C. | -(-3)与-|-3| | D. | $\frac{{2}^{2}}{3}$与($\frac{2}{3}$)2 |
13.一元二次方程3x2-2x+3=0的根的情况是( )
| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等的正实数根 | D. | 没有实数根 |
11.无论m为何实数,直线y=-x+2m与y=x+4的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 小时,求m的值.
小时,求m的值.
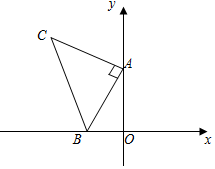 如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d). 如图,直线l的解析式为y=-$\frac{4}{3}$x+4,它与坐标轴分别交于A、B两点.
如图,直线l的解析式为y=-$\frac{4}{3}$x+4,它与坐标轴分别交于A、B两点.