题目内容
以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF,
(1)试探索BE和CF的关系?并说明理由.
(2)你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角.
见解析
解析试题分析:结论:(1)BE=CF
理由:因为∠FAB=∠EAC=90°∴∠FAB+∠BAC=∠EAC+∠BAC ,即:∠FAC=∠BAE
又∵AF=AB, AE=AC, ∴△FAC全等于△ BAE ∴BE=CF
(2) △FAC和△ BAE通过旋转得到,旋转中心为A点,旋转角为90°
考点:本题考查了全等三角形的判定
点评:此类试题属于难度较大的试题,考生解答此类试题时一定要把握好全等三角形的判定定理和旋转一定角度所得到图形的判定定理。

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.
17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N. 24、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
24、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF. 如图所示,以锐角△ABC的边AB为直径作⊙O,交AC,BC于E、D两点,若AC=14,CD=4,7sinC=3tanB,则BD=
如图所示,以锐角△ABC的边AB为直径作⊙O,交AC,BC于E、D两点,若AC=14,CD=4,7sinC=3tanB,则BD= 26、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
26、如图,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.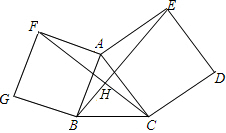 以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF
以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF