题目内容
矩形两条对角线相交的钝角为120°,若对角线长为2,则较短的一边长________.
1
分析:作出图形,根据矩形的对角线互相平分且相等求出对角线的一半的长,再求出对角线夹角的锐角为60°,然后判断出△ABO是等边三角形,根据等边三角形的三边都相等解答即可.
解答: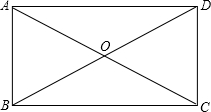 解:如图,∵矩形的对角线长为2,
解:如图,∵矩形的对角线长为2,
∴AO=BO= ×2=1,
×2=1,
∵AC、BD夹角的钝角为120°,
∴∠AOB=60°,
∴△ABO是等边三角形,
∴AB=AO=1,
即较短的一边长1.
故答案为:1.
点评:本题考查了矩形的对角线互相平分且相等的性质,等边三角形的判定与性质,熟记性质是解题的关键,作出图形更形象直观.
分析:作出图形,根据矩形的对角线互相平分且相等求出对角线的一半的长,再求出对角线夹角的锐角为60°,然后判断出△ABO是等边三角形,根据等边三角形的三边都相等解答即可.
解答:
 解:如图,∵矩形的对角线长为2,
解:如图,∵矩形的对角线长为2,∴AO=BO=
 ×2=1,
×2=1,∵AC、BD夹角的钝角为120°,
∴∠AOB=60°,
∴△ABO是等边三角形,
∴AB=AO=1,
即较短的一边长1.
故答案为:1.
点评:本题考查了矩形的对角线互相平分且相等的性质,等边三角形的判定与性质,熟记性质是解题的关键,作出图形更形象直观.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 10、如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=3,则该矩形两条对角线长度的和等于( )
10、如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=3,则该矩形两条对角线长度的和等于( )