题目内容
已知一次函数y=kx+b的图象与正比例函数y=
x交于点A,并与y轴交于点B(0,-4),点0为坐标原点,三角形AOB的面积为6,则一次函数的解析式为
| 1 |
| 3 |
y=-x-4或y=
x-4
| 5 |
| 3 |
y=-x-4或y=
x-4
.| 5 |
| 3 |
分析:根据题意,画出图形,根据三角形AOB的面积为6,求出A1、A2的坐标,用待定系数法求出一次函数的解析式即可.
解答: 解:如图,∵三角形AOB的面积为6,
解:如图,∵三角形AOB的面积为6,
∴
A1E•OB=6,
∵OB=4,
∴A1E=3,
代入正比例函数y=
x得,y=1,即A1(3,1),
设一次函数的解析式为y=kx+b,
则,
,
解得,
,
∴一次函数的解析式为y=
x-4;
同理可得,一次函数的另一个解析式为y=-x-4;
故答案为:y=-x-4或y=
x-4.
 解:如图,∵三角形AOB的面积为6,
解:如图,∵三角形AOB的面积为6,∴
| 1 |
| 2 |
∵OB=4,
∴A1E=3,
代入正比例函数y=
| 1 |
| 3 |
设一次函数的解析式为y=kx+b,
则,
|
解得,
|
∴一次函数的解析式为y=
| 5 |
| 3 |
同理可得,一次函数的另一个解析式为y=-x-4;
故答案为:y=-x-4或y=
| 5 |
| 3 |
点评:本题主要考查了两直线的相交、三角形的面积及用待定系数法求一次函数的解析式,注意不要漏解.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.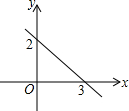 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.