题目内容
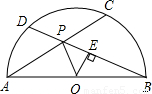
 如图,在直径为10的半圆AB上有两个动点C,D,弦AC、BD相交于点P,连接OP.
如图,在直径为10的半圆AB上有两个动点C,D,弦AC、BD相交于点P,连接OP.
(1)若BD=8,试求出圆心O到弦BD的距离OE的长度;
(2)试比较∠OPA和∠OPB的大小;(只写结论,不需证明)
(3)试求出AP•AC+BP•BD的值.
解:(1)∵OE⊥BD
∴ (1分)
(1分) (3分)
(3分)
(2)①若AC<BD,∠OPA>∠OPB
②若AC=BD,∠OPA=∠OPB
③若AC>BD,∠OPA<∠OPB
(3)连接AD,过P作PM⊥AB,垂足为M
则有∠ADB=∠PMB=90°,
又∠DBA=∠PBM
∴△ABD∽△PBM(11分)
∴
同理有
∴AP•AC=AB•AMBP•BD=AB•MB
∴AP•AC+BP•BD=AB•AM+AB•MB
=AB(AM+MB)
=AB2=100
分析:(1)构造直角三角形利用勾股定理求得OE的长即可;
(2)根据弦的大小关系判断弦所对的圆心角的大小关系即可,注意分类讨论.
(3)连接AD,过P作PM⊥AB,垂足为M证得△ABD∽△PBM后即可得到答案.
点评:本题考查了垂径定理及勾股定理的知识,题目中应用到了分类讨论思想.

练习册系列答案
相关题目
 如图,在直径为10的半圆AB上有两个动点C,D,弦AC、BD相交于点P,连接OP.
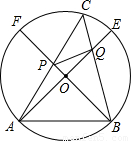
如图,在直径为10的半圆AB上有两个动点C,D,弦AC、BD相交于点P,连接OP.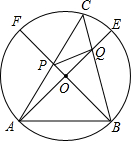 已知:如图,在直径为10的⊙O中,作两条互相垂直的直径AE和BF,在弧EF上取点C,弦AC交BF于P,弦CB交AE于Q,求证:四边形APQB的面积等于25.
已知:如图,在直径为10的⊙O中,作两条互相垂直的直径AE和BF,在弧EF上取点C,弦AC交BF于P,弦CB交AE于Q,求证:四边形APQB的面积等于25.