题目内容
在△ABC中,D、E分别是AB、AC的中点,若BC=4cm,则DE=________cm,S△ABC:S四边形BCED=________.
2 4:3
分析:三角形的中位线等于第三边的一半,那么第三边应等于中位线长的2倍,依此可以求出DE的长,根据三角形中位线定理可知△ADE∽△ABC相似且相似比是1:2,根据相似比求面积比.
解答: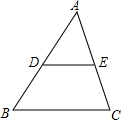 解:∵△ABC中,点D、E分别是边AB、AC的中点,
解:∵△ABC中,点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∵BC=4cm,
∴DE= BC=
BC= ×4=2cm.
×4=2cm.
∵D,E分别是AB,AC的中点,
∴DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=1:2,
∴△ADE与△ABC的面积之比为1:4,
∴△ABC与四边形BCED的面积之比是4:3.
故答案为:2,4:3.
点评:本题考查了三角形的中位线的性质:三角形的中位线等于第三边的一半.同时考查对相似三角形性质的理解,相似三角形面积的比等于相似比的平方.
分析:三角形的中位线等于第三边的一半,那么第三边应等于中位线长的2倍,依此可以求出DE的长,根据三角形中位线定理可知△ADE∽△ABC相似且相似比是1:2,根据相似比求面积比.
解答:
 解:∵△ABC中,点D、E分别是边AB、AC的中点,
解:∵△ABC中,点D、E分别是边AB、AC的中点,∴DE是△ABC的中位线,
∵BC=4cm,
∴DE=
 BC=
BC= ×4=2cm.
×4=2cm.∵D,E分别是AB,AC的中点,
∴DE∥BC,
∴△ADE∽△ABC,
∴AD:AB=1:2,
∴△ADE与△ABC的面积之比为1:4,
∴△ABC与四边形BCED的面积之比是4:3.
故答案为:2,4:3.
点评:本题考查了三角形的中位线的性质:三角形的中位线等于第三边的一半.同时考查对相似三角形性质的理解,相似三角形面积的比等于相似比的平方.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于