题目内容
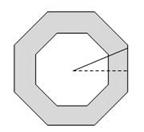
如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是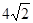 ,则可知大圆半径是(▲).
,则可知大圆半径是(▲).
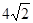 ,则可知大圆半径是(▲).
,则可知大圆半径是(▲). 
A.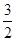 | B.3 | C.2 | D.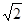 |
A
连接OB,过点C作CE⊥OB于点E,过点A作AF⊥OB与F,
设大圆的半径为r,则小圆的半径为r-1,
∵两个多边形均是正八边形,
∴∠AOB=45°,
∴AD=OA•sin45°= ,CE=
,CE= ,
,
∵阴影部分的面积是 ,
,
∴S四边形ACDB= =
= ,即S△AOB-S△COD=
,即S△AOB-S△COD= ,解得r=
,解得r=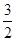 故选A.
故选A.

设大圆的半径为r,则小圆的半径为r-1,
∵两个多边形均是正八边形,
∴∠AOB=45°,
∴AD=OA•sin45°=
 ,CE=
,CE= ,
,∵阴影部分的面积是
 ,
,∴S四边形ACDB=
 =
= ,即S△AOB-S△COD=
,即S△AOB-S△COD= ,解得r=
,解得r=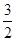 故选A.
故选A.
练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 ,
,
 三点共线;
三点共线; 成立,于是她得到这样的结论:如图(2),在
成立,于是她得到这样的结论:如图(2),在 中,
中, ,
, ,垂足为
,垂足为 ,设
,设 ,
, ,则有等式
,则有等式 成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.
成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.  .
.
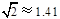 ,
,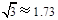 )
)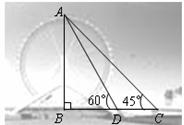
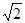 ≈1.41,
≈1.41, ≈1.73,
≈1.73,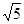 ≈2.24,
≈2.24, ≈2.45)
≈2.45)

 .
. .
.