题目内容
方程组 的所有正整数解是________.
的所有正整数解是________.

分析:首先根据题目已知条件
 与x、y、z为正整数,首先确定x的取值,再就x的各种情况进行讨论.得到最终结果.
与x、y、z为正整数,首先确定x的取值,再就x的各种情况进行讨论.得到最终结果.解答:∵
 ?
?
∵(y-z)2≥0?2yz≤y2+z2?2yz+y2+z2=2(y2+z2)?(y+z)2≤2(y2+z2)
∴(y+z)2=(6x-20)2≤2(y2+z2)=2(1979-x2)
于是(6x-20)2≤2(1979-x2)≤2×1978<632
注解到不等式(y+z)2≤2(y2+z2)有(y+z)2=(6x-20)2≤2(y2+z2)=2(1979-x2),
于是(6x-20)2≤2(1979-x2)≤2×1978<632,即-63<6x-20<63
又∵y+z=6x-20是正整数
∴0<6x-20<63,即
 ,从而4≤x≤13.
,从而4≤x≤13.再由y+z为偶数,从而y2+z2为偶数,x2为奇数,进而x为奇数.
∴x=5,7,9,11,13
①当x=5时,
 ,显然y、z正整数解不存在.
,显然y、z正整数解不存在.②当x=7时,
 ,显然y、z正整数解不存在.
,显然y、z正整数解不存在.③当x=9时,
 ,显然y、z正整数解不存在.
,显然y、z正整数解不存在.④当x=11时,解得
 或
或 ;
;⑤当x=13时,解得
 或
或 .
.故答案为

点评:本题考查高次方程,解题本题的突破口是首先确定x的取值范围.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
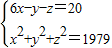 的所有正整数解是 .
的所有正整数解是 .