题目内容
梯形ABCD中,AD∥BC,那么它的四个内角的比∠A:∠B:∠C:∠D可以为
- A.1:2:4:5
- B.2:1:5:4
- C.4:2:1:5
- D.5:2:4:1
C
分析:根据四边形的四个角的和为360°及梯形中∠A与∠B及∠C与∠D互补,求出四个角,然后求出比.
解答: 解:由梯形的性质知,∠A与∠B互补,∠C与∠D互补,则,∠A与∠B的和,∠C与∠D的和均为180°,设四角的度数分别为:x,2x,4x,5x,由四边形的内角和为360°,得x+2x+4x+5x=360°,解得,四角分别为:30度,60度,120度,150度,同理B中的四角分别为:60度,30度,150度,120度,同理C中的四角分别为:120度,60度,30度,150度,同理D中的四角分别为:150度,60度,120度,30度,所以只有C中的满足∠A与∠B互补,∠C与∠D互补,选项C正确.故选C.
解:由梯形的性质知,∠A与∠B互补,∠C与∠D互补,则,∠A与∠B的和,∠C与∠D的和均为180°,设四角的度数分别为:x,2x,4x,5x,由四边形的内角和为360°,得x+2x+4x+5x=360°,解得,四角分别为:30度,60度,120度,150度,同理B中的四角分别为:60度,30度,150度,120度,同理C中的四角分别为:120度,60度,30度,150度,同理D中的四角分别为:150度,60度,120度,30度,所以只有C中的满足∠A与∠B互补,∠C与∠D互补,选项C正确.故选C.
点评:本题通过设适当的参数,根据四边形的内角和建立方程,求得各角的度数进行判定.
分析:根据四边形的四个角的和为360°及梯形中∠A与∠B及∠C与∠D互补,求出四个角,然后求出比.
解答:
 解:由梯形的性质知,∠A与∠B互补,∠C与∠D互补,则,∠A与∠B的和,∠C与∠D的和均为180°,设四角的度数分别为:x,2x,4x,5x,由四边形的内角和为360°,得x+2x+4x+5x=360°,解得,四角分别为:30度,60度,120度,150度,同理B中的四角分别为:60度,30度,150度,120度,同理C中的四角分别为:120度,60度,30度,150度,同理D中的四角分别为:150度,60度,120度,30度,所以只有C中的满足∠A与∠B互补,∠C与∠D互补,选项C正确.故选C.
解:由梯形的性质知,∠A与∠B互补,∠C与∠D互补,则,∠A与∠B的和,∠C与∠D的和均为180°,设四角的度数分别为:x,2x,4x,5x,由四边形的内角和为360°,得x+2x+4x+5x=360°,解得,四角分别为:30度,60度,120度,150度,同理B中的四角分别为:60度,30度,150度,120度,同理C中的四角分别为:120度,60度,30度,150度,同理D中的四角分别为:150度,60度,120度,30度,所以只有C中的满足∠A与∠B互补,∠C与∠D互补,选项C正确.故选C.点评:本题通过设适当的参数,根据四边形的内角和建立方程,求得各角的度数进行判定.

练习册系列答案
相关题目
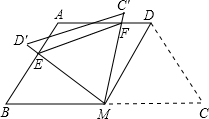 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点. DE.
DE. 如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.
如图,在梯形ABCD中,AD∥BC,AB=CD,点E在BC的延长线上,且∠BDE=∠ADC.求证:AB•BD=DE•AD.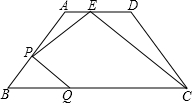 如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是
如图,在等腰梯形ABCD中,AD∥BC,AB=5,AD=6,BC=12,点E在AD边上,且AE:ED=1:2,点P是AB边上的一个动点,(P不与A,B重合)过点P作PQ∥CE交BC于点Q,设AP=x,CQ=y,则y与x之间的函数关系是 分别交边CD、BC于点F、E,若AD=3,BC=12,
分别交边CD、BC于点F、E,若AD=3,BC=12,