题目内容
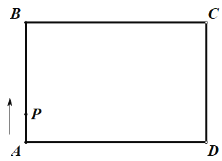
【题目】如图,在矩形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿着矩形的边顺时针方向运动一周回到点
出发,沿着矩形的边顺时针方向运动一周回到点![]() ,则点
,则点![]() 围成的图形面积
围成的图形面积![]() 与点
与点![]() 运动路程
运动路程![]() 之间形成的函数关系式的大致图象是( )
之间形成的函数关系式的大致图象是( )
A.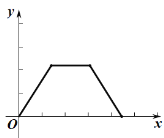 B.
B.
C.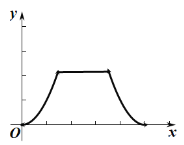 D.
D.
【答案】A
【解析】
分点P在AB上、点P在BC上、点P在CD上、点P在AD上四种情况,再分别根据直角三角形的面积公式、矩形的性质求出y与x的函数关系式,然后根据正比例函数、一次函数的图象特征即可得.
![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]()
设![]()
由题意,分以下四种情况:
(1)当点 P在AB上时,![]() ,此时有
,此时有![]()
则![]()
(2)当点P在BC上时,![]() ,即
,即![]()
![]()
![]() ,即
,即![]()
![]()
则![]()
(3)当点P在CD上时,![]() ,即
,即![]()
![]()
![]() ,即
,即![]()
![]()
![]()
则![]()
(4)当点P在AD上时,![]() ,即
,即![]()
![]()
![]() ,即
,即![]()
![]()
此时,点![]() 在一条直线上,则
在一条直线上,则![]()
综上,![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为
由正比例函数和一次函数的图象特征可知,只有A选项符合题意
故选:A.

【题目】我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量![]() (万件与月份
(万件与月份![]() (月)的关系为:
(月)的关系为: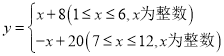
每件产品的利润![]() (元)与月份
(元)与月份![]() (月)的关系如下表:
(月)的关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() 请你根据表格直接写出每件产品利润z (元) 与月份
请你根据表格直接写出每件产品利润z (元) 与月份![]() (月)的函数关系式;
(月)的函数关系式;
![]() 若月利润
若月利润![]() (万元) =当月销售量
(万元) =当月销售量![]() (万件)
(万件) ![]() 当月每件产品的利润
当月每件产品的利润![]() (元),求月利润
(元),求月利润![]() (万元)与月份
(万元)与月份![]() (月)的关系式;
(月)的关系式;
![]() 当
当![]() 为何值时,月利润
为何值时,月利润![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.