题目内容
已知a2+b2=1, ,求a+b+ab的取值范围.
,求a+b+ab的取值范围.
解:∵a2+b2=(a+b)2-2ab,a2+b2=1,
∴ab=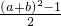 ,
,
设a+b=t,则- ≤t≤
≤t≤ ,
,
∴y=a+b+ab=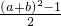 +a+b=
+a+b= (t2-1)+t=
(t2-1)+t= t2+t-
t2+t- =
= (t+1)2-1,
(t+1)2-1,
∴t=-1时,y有最小值为-1,
t= 时,y有最大值,此时y=
时,y有最大值,此时y= (
( +1)2-1=
+1)2-1=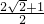 ,
,
∴-1≤y≤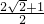 ,
,
即a+b+ab的取值范围为-1≤a+b+ab≤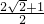 .
.
分析:由a2+b2=(a+b)2-2ab,a2+b2=1得到ab=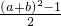 ,设a+b=t,则-
,设a+b=t,则- ≤t≤
≤t≤ ,于是得到=a+b+ab=
,于是得到=a+b+ab=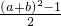 +a+b=
+a+b= (t2-1)+t,配成顶点式为y=
(t2-1)+t,配成顶点式为y= (t+1)2-1,根据二次函数的最值问题和性质得到t=-1时,y有最小值为-1;t=
(t+1)2-1,根据二次函数的最值问题和性质得到t=-1时,y有最小值为-1;t= 时,y有最大值,此时y=
时,y有最大值,此时y= (
( +1)2-1,由此得到a+b+ab的取值范围.
+1)2-1,由此得到a+b+ab的取值范围.
点评:本题考查了二次函数的最值问题:先把二次函数配成顶点式:y=a(x-h)2+k,当a<0时,x=h,y有最大值k;当a>0,x=h,y有最小值k.也考查了二次函数的性质.
∴ab=
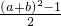 ,
,设a+b=t,则-
 ≤t≤
≤t≤ ,
,∴y=a+b+ab=
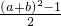 +a+b=
+a+b= (t2-1)+t=
(t2-1)+t= t2+t-
t2+t- =
= (t+1)2-1,
(t+1)2-1,∴t=-1时,y有最小值为-1,
t=
 时,y有最大值,此时y=
时,y有最大值,此时y= (
( +1)2-1=
+1)2-1=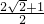 ,
,∴-1≤y≤
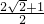 ,
,即a+b+ab的取值范围为-1≤a+b+ab≤
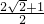 .
.分析:由a2+b2=(a+b)2-2ab,a2+b2=1得到ab=
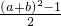 ,设a+b=t,则-
,设a+b=t,则- ≤t≤
≤t≤ ,于是得到=a+b+ab=
,于是得到=a+b+ab=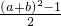 +a+b=
+a+b= (t2-1)+t,配成顶点式为y=
(t2-1)+t,配成顶点式为y= (t+1)2-1,根据二次函数的最值问题和性质得到t=-1时,y有最小值为-1;t=
(t+1)2-1,根据二次函数的最值问题和性质得到t=-1时,y有最小值为-1;t= 时,y有最大值,此时y=
时,y有最大值,此时y= (
( +1)2-1,由此得到a+b+ab的取值范围.
+1)2-1,由此得到a+b+ab的取值范围.点评:本题考查了二次函数的最值问题:先把二次函数配成顶点式:y=a(x-h)2+k,当a<0时,x=h,y有最大值k;当a>0,x=h,y有最小值k.也考查了二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a2+b2=25,且ab=12,则a+b的值是( )
A、
| ||
B、±
| ||
| C、7 | ||
| D、±7 |