题目内容
 已知,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:FB=EC.
已知,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:FB=EC.
证明:在Rt△AEF和Rt△ABF中,
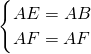 ,
,
∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB= ∠BCD=45°,
∠BCD=45°,
在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC.
分析:通过△AEF≌△ABF,可以求证FE=FB,然后证得△CEF为等腰直角三角形即可.
点评:本题考查了全等三角形的证明,考查了等腰直角三角形的判定,本题求证Rt△AEF≌Rt△ABF是解本题的关键.
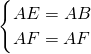 ,
,∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB=
 ∠BCD=45°,
∠BCD=45°,在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC.
分析:通过△AEF≌△ABF,可以求证FE=FB,然后证得△CEF为等腰直角三角形即可.
点评:本题考查了全等三角形的证明,考查了等腰直角三角形的判定,本题求证Rt△AEF≌Rt△ABF是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
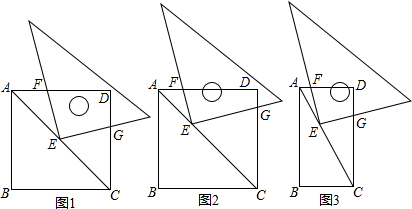
 已知,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:FB=EC.
已知,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F,求证:FB=EC.