题目内容
如图，将边长为4的正方形纸片，置于平面直角坐标系内，顶点A在坐标原点，点B在x轴的正半轴上，E、F分
别是AD、BC的中点，点M在DC上．将△ADM沿AM折叠，点D折叠后恰好落在EF上的点P处．（1）求∠EAP的度数；
（2）求折痕AM所在直线的函数关系式；
（3）设H为直线AM上的点，是否存在这样的点H，使得以H、A、P为顶点的三角形是等腰三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
分析：在直角三角形APE中，利用锐角三角函数求得∠EAP的度数即可．
解答：解：
（1）在Rt△AEP中，AE=2，AP=4，
∴cos∠EAP=
=
．
∴∠EAP=60°．
（2）∵翻折，且∠EAP=60°，∴∠DAM=∠MAP=30°．
∴DM=ADtan30°=
．
∴M（
，4）．
∴折痕AM所在直线的函数关系式为y=
x．（6分）
（3）H点的坐标为：
（-2，-2
）或（
，2）或（2，2
）或（2
，6）．（10分）
（1）在Rt△AEP中，AE=2，AP=4，
∴cos∠EAP=
| AE |
| AP |
| 1 |
| 2 |
∴∠EAP=60°．
（2）∵翻折，且∠EAP=60°，∴∠DAM=∠MAP=30°．
∴DM=ADtan30°=
| 4 |
| 3 |
| 3 |
∴M（
| 4 |
| 3 |
| 3 |
∴折痕AM所在直线的函数关系式为y=
| 3 |
（3）H点的坐标为：
（-2，-2
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
点评：本题考查了一次函数的综合知识，题目难度适中，此类题目常出现在中考题的倒数第2-3题上．
练习册系列答案
口算题天天练系列答案
相关题目
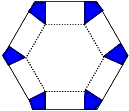如图，将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形，再沿虚线折起，做成一个无盖直六棱柱纸盒，使侧面积等于底面积，被剪去的六个四边形的面积和为如图，将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2013•丰南区一模）如图，将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为