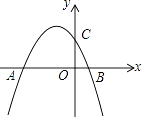题目内容
【题目】如图，图中二次函数解析式为y=ax2+bx+c（a≠0）则下列命题中正确的有（填序号）
①abc＞0；②b2＜4ac；③4a﹣2b+c＞0；④2a+b＞c．
【答案】①③④
【解析】解：①∵抛物线开口向上，抛物线的对称轴在y轴右侧，抛物线与y轴交于y轴负半轴，
∴a＞0，﹣ 
＞0，c＜0，
∴b＜0，abc＞0，①正确；
②∵抛物线与x轴有两个不同交点，
∴△=b2﹣4ac＞0，b2＞4ac，②错误；
③当x=﹣2时，y=4a﹣2b+c＞0，③正确；
④∵0＜﹣ ＜1，
∴﹣2a＜b＜0，
∴2a+b＞0＞c，④正确．
所以答案是：①③④．
【考点精析】认真审题，首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）)，还要掌握命题与定理(我们把题设、结论正好相反的两个命题叫做互逆命题．如果把其中一个叫做原命题，那么另一个叫做它的逆命题；经过证明被确认正确的命题叫做定理)的相关知识才是答题的关键．
练习册系列答案
名校课堂系列答案
相关题目
