题目内容
(2004•石景山区模拟)已知:如图,BC是半圆O的直径,D、E是半圆O上两点,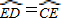 ,CE的延长线与BD的延长线交于点A,过点E作EF⊥BC于点F,交CD与点G.
,CE的延长线与BD的延长线交于点A,过点E作EF⊥BC于点F,交CD与点G.(1)求证:AE=DE;
(2)若AE=
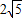 ,cot∠ABC=
,cot∠ABC= ,求DG.
,求DG.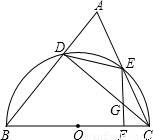
【答案】分析:(1)由圆周角定理及直角三角形的性质可得到∠A=∠ADE,再根据等角对等边即可求得结论.
(2)连接BE,根据已知及相似三角形的判定得到△ECG∽△DCE,根据相似三角形的对应边成比例即可求得CG,DG的值.
解答: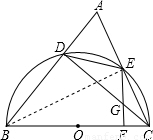 (1)证明:∵BC是半圆O直径,
(1)证明:∵BC是半圆O直径,
∴∠ADC=∠BDC=90°.
∵ ,
,
∴∠EDC=∠ECD.
∴∠A=∠ADE.
∴AE=DE.(3分)
(2)解:连接BE,
∵ ,
,
∴DE=EC.
∴AE=EC=2 .
.
∵BC是半圆O直径,
∴∠BEC=90°即BE⊥AC.
∴BA=BC.
∵Rt△BDC中,cot∠ABC= ,
,
设BD=3x,CD=4x,则BC=5x,
∴AB=BC=5x,AD=2x.
∵AE•AC=AD•AB,
∴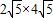 =2x•5x.
=2x•5x.
解得:x=2,即CD=8.(6分)
∵EF⊥BC,
∴∠CEF+∠ECB=90°.
∵B,C,E,D四点共圆,
∴∠ADE=∠ECB.
又∵∠EDC+∠ADE=90°,
∴∠CEF=∠EDC.
∵∠DCE为公共角,
∴△ECG∽△DCE.
∴ .
.
∴GC=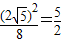 .
.
∴DG=8-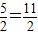 .(8分)
.(8分)
点评:本题考查圆周角定理,相似三角形的判定,直角三角形的性质等知识点的综合运用.
(2)连接BE,根据已知及相似三角形的判定得到△ECG∽△DCE,根据相似三角形的对应边成比例即可求得CG,DG的值.
解答:
 (1)证明:∵BC是半圆O直径,
(1)证明:∵BC是半圆O直径,∴∠ADC=∠BDC=90°.
∵
 ,
,∴∠EDC=∠ECD.
∴∠A=∠ADE.
∴AE=DE.(3分)
(2)解:连接BE,
∵
 ,
,∴DE=EC.
∴AE=EC=2
 .
.∵BC是半圆O直径,
∴∠BEC=90°即BE⊥AC.
∴BA=BC.
∵Rt△BDC中,cot∠ABC=
 ,
,设BD=3x,CD=4x,则BC=5x,
∴AB=BC=5x,AD=2x.
∵AE•AC=AD•AB,
∴
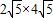 =2x•5x.
=2x•5x.解得:x=2,即CD=8.(6分)
∵EF⊥BC,
∴∠CEF+∠ECB=90°.
∵B,C,E,D四点共圆,
∴∠ADE=∠ECB.
又∵∠EDC+∠ADE=90°,
∴∠CEF=∠EDC.
∵∠DCE为公共角,
∴△ECG∽△DCE.
∴
 .
.∴GC=
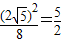 .
.∴DG=8-
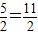 .(8分)
.(8分)点评:本题考查圆周角定理,相似三角形的判定,直角三角形的性质等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 S△ABC?若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,求出点P的坐标;若不存在,请说明理由.