题目内容
 (2012•泰州)如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-
(2012•泰州)如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-| 2 | 3 |
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
分析:(1)根据正方形的性质得出点B、C的坐标,然后利用待定系数法求函数解析式解答;
(2)令y=0求出二次函数图象与x轴的交点坐标,再根据y>0,二次函数图象在x轴的上方写出x的取值范围即可.
(2)令y=0求出二次函数图象与x轴的交点坐标,再根据y>0,二次函数图象在x轴的上方写出x的取值范围即可.
解答:解:(1)∵正方形OABC的边长为2,
∴点B、C的坐标分别为(2,2),(0,2),
∴
,
解得
,
∴二次函数的解析式为y=-
x2+
x+2;
(2)令y=0,则-
x2+
x+2=0,
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
∴二次函数与x轴的交点坐标为(-1,0)、(3,0),
∴当y>0时,x的取值范围是-1<x<3.
∴点B、C的坐标分别为(2,2),(0,2),
∴
|
解得
|
∴二次函数的解析式为y=-
| 2 |
| 3 |
| 4 |
| 3 |
(2)令y=0,则-
| 2 |
| 3 |
| 4 |
| 3 |
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
∴二次函数与x轴的交点坐标为(-1,0)、(3,0),
∴当y>0时,x的取值范围是-1<x<3.
点评:本题综合考查了二次函数,正方形的性质,待定系数法求函数解析式,根据正方形的性质求出点B、C的坐标是解题的关键,也是本题的突破口,本题在此类题目中比较简单.

练习册系列答案
相关题目
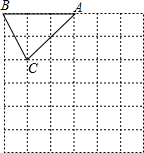 (2012•泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(2012•泰州)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2. (2012•泰州)如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是
(2012•泰州)如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是 (2012•泰州)如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是
(2012•泰州)如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是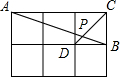 (2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是
(2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.