题目内容
 如图,在等腰△ABC中,AB=AC,点D在BC上,且AD=AE.
如图,在等腰△ABC中,AB=AC,点D在BC上,且AD=AE.
(1)若∠BAC=90°,∠BAD=30°,求∠EDC的度数?
(2)若∠BAC=a(a>30°),∠BAD=30°,求∠EDC的度数?
(3)猜想∠EDC与∠BAD的数量关系?(不必证明)
(1)解:∵∠BAC=90°,AB=AC,
∴∠B=∠C= (180°-∠BAC)=45°,
(180°-∠BAC)=45°,
∴∠ADC=∠B+∠BAD=45°+30°=75°,
∵∠DAC=∠BAC-∠BAD=90°-30°=60°,
∵AD=AE,
∴∠ADE=∠AED= (180°-∠DAC)=60°,
(180°-∠DAC)=60°,
∴∠EDC=∠ADC-∠ADE=75°-60°=15°,
答:∠EDC的度数是15°.
(2)解:与(1)类似:∠B=∠C= (180°-∠BAC)=90°-
(180°-∠BAC)=90°- α,
α,
∴∠ADC=∠B+∠BAD=90°- α+30°=120°-
α+30°=120°- α,
α,
∵∠DAC=∠BAC-∠BAD=α-30°,
∴∠ADE=∠AED= (180°-∠DAC)=105°-
(180°-∠DAC)=105°- α,
α,
∴∠EDC=∠ADC-∠ADE=(120°- α)-(105°-
α)-(105°- α)=15°,
α)=15°,
答:∠EDC的度数是15°.
(3)∠EDC与∠BAD的数量关系是∠EDC= ∠BAD.
∠BAD.
分析:(1)根据等腰三角形性质求出∠B的度数,根据三角形的外角性质求出∠ADC,求出∠DAC,根据等腰三角形性质求出∠ADE即可;
(2)根据等腰三角形性质求出∠B的度数,根据三角形的外角性质求出∠ADC,求出∠DAC,根据等腰三角形性质求出∠ADE即可;
(3)根据(1)(2)的结论猜出即可.
点评:本题主要考查学生运用等腰三角形性质,三角形的内角和定理,三角形的外角性质进行推理的能力,题目比较典型,是一道很好的题目,关键是进行推理和总结规律.
∴∠B=∠C=
 (180°-∠BAC)=45°,
(180°-∠BAC)=45°,∴∠ADC=∠B+∠BAD=45°+30°=75°,
∵∠DAC=∠BAC-∠BAD=90°-30°=60°,
∵AD=AE,
∴∠ADE=∠AED=
 (180°-∠DAC)=60°,
(180°-∠DAC)=60°,∴∠EDC=∠ADC-∠ADE=75°-60°=15°,
答:∠EDC的度数是15°.
(2)解:与(1)类似:∠B=∠C=
 (180°-∠BAC)=90°-
(180°-∠BAC)=90°- α,
α,∴∠ADC=∠B+∠BAD=90°-
 α+30°=120°-
α+30°=120°- α,
α,∵∠DAC=∠BAC-∠BAD=α-30°,
∴∠ADE=∠AED=
 (180°-∠DAC)=105°-
(180°-∠DAC)=105°- α,
α,∴∠EDC=∠ADC-∠ADE=(120°-
 α)-(105°-
α)-(105°- α)=15°,
α)=15°,答:∠EDC的度数是15°.
(3)∠EDC与∠BAD的数量关系是∠EDC=
 ∠BAD.
∠BAD.分析:(1)根据等腰三角形性质求出∠B的度数,根据三角形的外角性质求出∠ADC,求出∠DAC,根据等腰三角形性质求出∠ADE即可;
(2)根据等腰三角形性质求出∠B的度数,根据三角形的外角性质求出∠ADC,求出∠DAC,根据等腰三角形性质求出∠ADE即可;
(3)根据(1)(2)的结论猜出即可.
点评:本题主要考查学生运用等腰三角形性质,三角形的内角和定理,三角形的外角性质进行推理的能力,题目比较典型,是一道很好的题目,关键是进行推理和总结规律.

练习册系列答案
相关题目
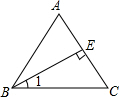 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
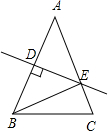 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=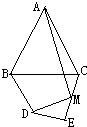 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.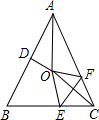 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是