题目内容
已知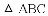
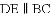
A. 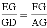 ; B.
; B. 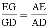 ; C.
; C. 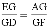 ; D.
; D. 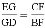 .
.
练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
题目内容
已知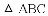
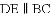
A. 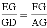 ; B.
; B. 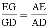 ; C.
; C. 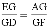 ; D.
; D. 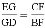 .
.
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案