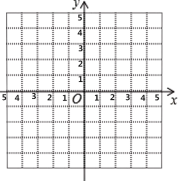
题目内容
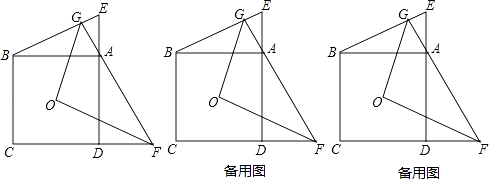
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() 三点.
三点.
(1)在平面直角坐标中画出![]() ,求
,求![]() 的面积
的面积
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() 使得
使得![]() 的面积等于
的面积等于![]() 的面积?若存在,求出点
的面积?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
(3)如果在第二象限内有一点![]() ,用含
,用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(4)且四边形![]() 的面积是
的面积是![]() 的面积的三倍,是否存在点
的面积的三倍,是否存在点![]() ,若存在,求出满足条件的
,若存在,求出满足条件的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)图见解析;![]() ,(2)存在;
,(2)存在;![]() 或
或![]() ,(3)
,(3)![]() ,(4)存在;
,(4)存在;![]()
【解析】
(1)根据坐标画出图形,依据三角形面积计算公式计算即可.
(2)分两种情况讨论使得![]() 的面积等于
的面积等于![]() 的面积的点
的面积的点![]() ,①当点在
,①当点在![]() 点
点![]() 的左边时,设存在点
的左边时,设存在点![]() ,根据
,根据![]() ,
,![]() 进行求解;②当点在
进行求解;②当点在![]() 点
点![]() 的右边时,设存在点
的右边时,设存在点![]() ,根据
,根据![]() ,
,![]() 进行求解.
进行求解.
(3)根据![]() 计算即可,注意
计算即可,注意![]() 这个限制条件.
这个限制条件.
(4)在(3)的基础上,根据![]() ,列方程计算即可.
,列方程计算即可.
(1)如图1,在平面直角坐标中画出![]() ,
,

图1
![]() 的面积为:
的面积为:![]() .
.
(2)在![]() 轴上存在点
轴上存在点![]() ,使得
,使得![]() 的面积等于
的面积等于![]() 的面积.分两种情况讨论:
的面积.分两种情况讨论:
①当点在![]() 点
点![]() 的左边时,设存在点
的左边时,设存在点![]() ,使得
,使得![]() ,
,
∵![]() ,
,
又由(1)得,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
即点![]() 坐标为
坐标为![]() .
.
②当点在![]() 点
点![]() 的右边时,设存在点
的右边时,设存在点![]() ,使得
,使得![]() ,
,
∵![]() ,
,
又由(1)得,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
即点![]() 坐标为
坐标为![]() .
.
综上所得,在![]() 轴上存在点
轴上存在点![]() 使得
使得![]() 的面积等于
的面积等于![]() 的面积,点
的面积,点![]() 坐标为
坐标为![]() 或
或![]() .
.
(3)如图2,作出点![]() ,连接
,连接![]() ,
,![]() ,四边形
,四边形![]() 的面积可以看作是
的面积可以看作是![]() 和
和![]() 的面积之和,
的面积之和,

图2
∵点![]() 在第二象限内,
在第二象限内,
∴![]() ,四边形
,四边形![]() 的面积为:
的面积为:
![]()
![]()
![]()
![]()
则四边形![]() 的面积为
的面积为![]() .
.
(4)存在点![]() ,使四边形
,使四边形![]() 的面积是
的面积是![]() 的面积的三倍,
的面积的三倍,
则![]() ,
,
解得![]() ,满足条件,
,满足条件,
即存在点![]() ,使四边形
,使四边形![]() 的面积是
的面积是![]() 的面积的三倍.
的面积的三倍.

练习册系列答案
相关题目