题目内容
在tan30°,-3.14, ,0.101001,
,0.101001,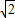 ,π中,其中无理数是 .
,π中,其中无理数是 .
【答案】分析:根据无理数的定义解答.
解答:解:tan30°= ,是无理数;
,是无理数;
 ,π也是无理数;
,π也是无理数;
故答案为tan30°, ,π.
,π.
点评:熟记特殊角的三角函数值和无理数的定义是解决本题的关键.
解答:解:tan30°=
 ,是无理数;
,是无理数; ,π也是无理数;
,π也是无理数;故答案为tan30°,
 ,π.
,π.点评:熟记特殊角的三角函数值和无理数的定义是解决本题的关键.

练习册系列答案
相关题目
 ,cos30°=
,cos30°=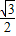 ,tan30°=
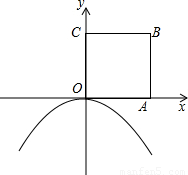
,tan30°=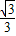 .)
.)
 ,cos30°=
,cos30°=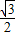 ,tan30°=
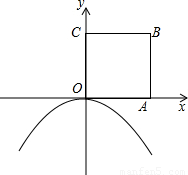
,tan30°=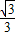 .)
.)
 ,cos30°=
,cos30°=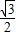 ,tan30°=
,tan30°=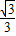 .)
.)
 ,cos30°=
,cos30°=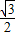 ,tan30°=
,tan30°=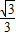 .)
.)