题目内容
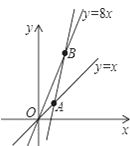
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b(a>0,b>0).设直线AB的解析式为y=kx+m,若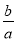 是整数时,k也是整数,满足条件的k值共有 个.
是整数时,k也是整数,满足条件的k值共有 个.
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
题目内容
如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b(a>0,b>0).设直线AB的解析式为y=kx+m,若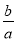 是整数时,k也是整数,满足条件的k值共有 个.
是整数时,k也是整数,满足条件的k值共有 个.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案