题目内容
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
(1)求证:△ABD∽△CED ;
(2)若AB=6,AD=2CD,求BE的长.
 |
(1)证明:∵ △ABC是等边三角形
∴ ∠BAC=∠ACB=60°.∠ACF=120°.……………1分
∵ CE是外角平分线, ∴ ∠ACE=60°.………2分
 ∴ ∠BAC=∠ACE.……………… 3分
∴ ∠BAC=∠ACE.……………… 3分
又∵ ∠ADB=∠CDE,
∴ △ABD∽△CED. ……………… 4分
![]()
![]()
![]()
|
∴ AM=CM=3,BM=AB·sin60°=
∵ AD=2CD,∴ CD=2,AD=4,MD=1.
在Rt△BDM中, ……………………… 6分
由(1)△ABD∽△CED得, , , ∴ED=
∴ BE=BD+ED=![]() .…………… 8分
.…………… 8分

练习册系列答案
相关题目
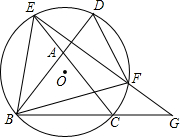 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.